Le champ électrique créé par un dipôle
Les conditions expérimentales \(a \ll r\) rendent mal aisée la détermination du champ électrique résultant à partir de la somme géométrique des champs engendrés par chaque charge \(+ q\) et \(- q\). Comme nous l'avons vu au paragraphe 2.5.1, il sera désormais plus pertinent de déterminer le champ électrique en dérivant la fonction potentielle créée par l'ensemble des charges.
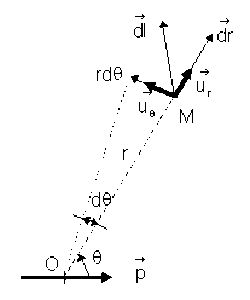
Dans le cas du dipôle, la symétrie de révolution autour de l'axe formé par les 2 charges, nous amène à utiliser les coordonnées polaires \(r\) et \(\theta\) telles que nous les avons déjà définies sur la figure ci-dessous.
Soit le point \(M\) défini par ses coordonnées \(r\) et \(\theta\) . Déplaçons nous à partir de \(M\) d'un déplacement élémentaire \(\mathrm d l\). Ce déplacement élémentaire peut toujours se décomposer en une somme de deux vecteurs qui font apparaître explicitement les variables polaires \(r\) et \(\theta\) . Nous avons en effet :
\(\mathrm d \vec l = \mathrm d \vec r + r \mathrm d \vec \theta\)
On précisera du même coup les vecteurs unitaires \(\vec u_r\) et \(\vec u_{\theta}\) ayant pour origine \(M\), qui permettent de définir :
\(\mathrm d \vec l = \mathrm d r ~ \times ~ \vec u_r ~ + ~ r \mathrm d \theta ~\times~ \vec u_{\theta}\)
Dans le repère de coordonnées polaires le vecteur champ électrique a pour composantes \(E_r\) et \(E_\theta\) . Ainsi lorsque nous formons le produit scalaire
\(\vec E . \mathrm d \vec l\) , il vient :
\(\vec E . \mathrm d \vec l = E_r \mathrm d r ~ + ~ E_\theta \mathrm d \theta\)
Calculons d'autre part, toujours dans le repère en coordonnées polaires, la différentielle totale de la fonction potentielle \(V\). Nous avons :
\(\mathrm d V = \frac{\partial V}{\partial r} \mathrm d r ~ + ~ \frac{\partial V}{\partial \theta} \mathrm d \theta\)
Comme nous l'avons déjà vu à propos des coordonnées cartésiennes, on obtient les cordonnées du champ électrique par identification.
Nous avons : \(\vec E = \left\{ \begin{array}{c} \displaystyle{-\frac{\partial V}{\partial r}} \\\\ \displaystyle{-\frac{1}{r} \frac{\partial V}{\partial \theta}} \end{array}\right.\)
En nous reportant à l'expression de la fonction potentielle,
\(V(M) ~ \# ~ \frac{q}{4 \pi \epsilon_0} \frac{a.\cos \theta}{r^2} ~ \# ~ \frac{p}{4 \pi \epsilon_0} \frac{\cos \theta}{r^2}\) ,
il vient : \(\vec E = \left\{ \begin{array}{c} \displaystyle{E_r = \frac{2 k p . \cos \theta}{r^3}} \\\\ \displaystyle{E_q = \frac{k p . \sin \theta}{r^3}} \end{array}\right.\)
Précisons encore une fois que le vecteur champ électrique est défini dans le repère de coordonnées polaires par :
\(\vec E = \frac{2 k p . \cos \theta}{r^3} ~ \vec u_r ~ + ~ \frac{k p . \sin \theta}{r^3} ~ \vec u_\theta\)
Le module du vecteur champ électrique a pour valeur :
\(|\vec E| = \frac{kp}{r^3} \sqrt{1 + 3 \cos^2 \theta}\)
L'argument \(\theta\) du vecteur \(OM\) fixe le rapport entre les deux composantes du champ électrique puisque l'on a :
\(\frac{E_\theta}{E_r} = \frac{1}{2} \tan \theta\) .
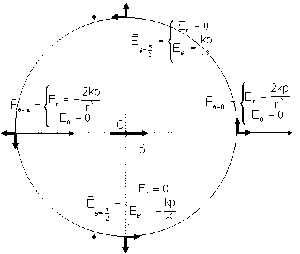
Exercice résolu : Déterminer et représenter sur un cercle de rayon \(r\) pour différentes valeurs de \(\theta = 0\), \(p/2\), \(p\) et \(- p/2\), le vecteur champ électrique créé par un dipôle \(p = q.a\).
Les composantes \(E_r\) et \(E_\theta\) du champ électrique s'obtiennent facilement en donnant la valeur de l'angle \(\theta\) .
On portera ici la plus grande attention à l'orientation en chaque point singulier du repère \(\vec u_r\), \(\vec u_\theta\), qui fixe le sens de \(E_r\) et \(E_\theta\) . On notera également l'importance de la symétrie dans ce problème.