Composition de vibrations (3)
Partie
Question
Soient trois vibrations sinusoïdales de même amplitude et déphasées entre elles de \(\phi\). Calculer l'intensité résultante par les nombres complexes.
Aide simple
Exprimer les trois vibrations sinusoïdales sous forme de nombres complexes.
Rappel de cours
Nombre complexes :
Définition: on appelle nombre complexe un nombre z tel que: \(z = a + i b\) avec a et b nombre réels et \(i^2=-1\)
Le module r est défini par: \(r^2=a^2+b^2= ( a + i b ) ( a - i b )\)
\(z=a-ib\) est le conjugué de z
L'argument \(\theta\) est défini par \(tan\theta=\frac{b}{a}\) ; \(sin\theta=\frac{b}{r}\) ; \(cos\theta=\frac{b}{r}\)
On peut donc écrire : \(z= r (cos\theta+i\,sin\theta)\)
On remarque que pour :
\(z_1=r_1(cos\theta_1+i\,sin\theta_1)\) et \(z_2=r_2(cos\theta_2+i\,sin\theta_2)\) on a :
\(Z=z_1z_2=r_1r_2[cos(\theta_1+\theta_2)+i\,sin (\theta_1+\theta_2)]\)
soit : \(Z=rcos(\theta+i\,sin\theta)\)
d'où : \(r=r_1.r_2\)
\(\theta=\theta_1+\theta_2\)
Un nombre complexe peut aussi s'écrire en notation exponentielle :
\(z=r\,e^{i\theta}\) avec \(e^{i\,\theta}=cos\theta+i\,sin\theta\)
on a donc \(cos\theta=\frac{e^{i\,\theta}+e^{-i\,\theta}}{2}\) et \(sin\theta=\frac{e^{i\,\theta}- e^{-i\,\theta}}{2}\)
pour \(\theta=\pi\) on a : \(e^{i\pi}=-1\)
pour \(\theta=2\,\pi\) on a : \(e^{i2\pi}=1\)
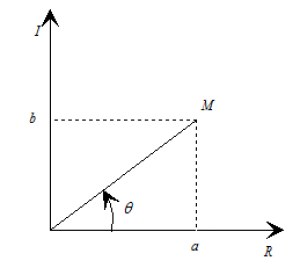
Représentation d'un nombre complexe dans le plan complexe :
Soient R l'axe des réels et I l'axe des imaginaires.
Soit \(z=a+i\,b\) la droite passant par O et M qui fait un angle \(\theta\) avec l'axe réel et le segment OM a pour longueur: \(r=\sqrt{a^2+b^2}\).
La multiplication de z par un nombre complexe de module égal à 1 et d'argument \(\theta'\) se traduit par une rotation de OM d'un angle \(\theta'\) dans le sens direct.
Solution détaillée
soit \(z_1=a\,e^{(i\omega t+\phi)}\) avec \(s_1=Re(z_1)\) où \(s_1=Re(z_1)\) est la partie réelle de \(z_1\)
soient également \(z_2=e^{(i\omega t)}\) et \(z_3=e^{(i\omega t-\phi)}\)
alors \(z_r=z_1+z_2+z_3=a\,e^{i\omega t}(e^{-i\phi}+e^{i\phi}+1)\)
si \(\overline{z_r}\) est le complexe conjugué de \(z_r\) alors \(I_r=z_r.\overline z_r=a\,e^{i\omega t}(2cos\phi+1)a\,e^{-i\omega t}(2cos\phi+1)\)
\(I_r=a^2(2cos\phi+1)^2=a_r^2\)
et \(s_r=Re(z_r)=a(2cos\phi+1)=a_rcos(\omega t+\Phi)\)
d'où \(a_r=(2cos\phi+1)\) et \(\Phi=0\)