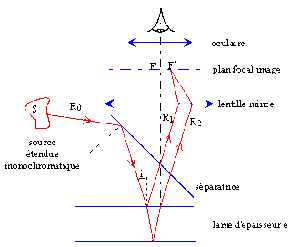
Dispositif d'observation (cas des lames à faces parallèles en lumière monochromatique)
Cas des lames à faces parallèles en lumière monochromatique
Considérons le dispositif ci-contre.
Tous les rayons issus de la source étendue et parallèles au rayon \(R_0\) vont être réfléchis sur la lame séparatrice et vont arriver sur la lame mince sous une même incidence \(i\). Ils viendront donc tous converger en un même foyer image secondaire de la lentille \(F'\). Si l'on observe le phénomène dans le plan focal de la lentille constituant l'objectif, l'axe de la lentille constitue un axe de révolution pour la figure d'interférences et les anneaux sont centrés sur le foyer principal image \(F'\) de l'objectif.
L'oculaire permet une observation visuelle des anneaux très serrés dans le plan focal de l'objectif
Démonstration : Calcul du rayon des anneaux par réflexion:
Introduisons l'ordre d'interférence \(p\). C'est, par définition, un nombre quelconque tel que:
\(p = \frac{\delta}{\lambda} = \frac{2 n e \cos r}{\lambda} + \frac{1}{2}\)
Soit \( p_{i = 0}\) l'ordre d'interférence sous incidence normale (i=0) : \( p_{i=0} = \frac{2 n e}{\lambda} + \frac{1}{2}\)
On remarque que \(p_{i = 0}\) est la valeur maximale de \(p\) (donc \(p_0 \ge p\) ) et \(p_{i = 0}\)peut prendre une valeur quelconque. L'ordre d'interférence \(p\) décroît à partir du centre de la figure car \(\cos r\) diminue quand \(i\) (donc\(r\)) augmente.
Prenons un exemple : \(e = 0.1 \mathrm{ mm} , \quad l = 0.56 \mathrm{ mm }\) alors \(p_{i = 0} = 178.57 + 0.5 = 179.07\)
Le premier anneau sombre est obtenu lorsque: \(p_1 = \frac{2 n e \cos r_1}{\lambda} + \frac{1}{2}\)
\(p_1\) est le premier nombre entier \(\mathrm{+1/2 }\) immédiatement inférieur à \(p_{i=0}\)
Pour le deuxième anneau : \(p_2 = p_1 - 1\)
Pour le \(N\)ième anneau: \(pN = p_1 - (N - 1 )\)
Continuons l'exemple précédent :
\(pl = 178,5 ; p_2 = 177,5 ; p_N = 178,5 - (N - 1) = 179,5 - N\). On a donc:
\(p_N - p_1 = 1 - N = \frac{2 n e \cos r_N}{\lambda} - \frac{2 n e \cos r_1}{\lambda}\)
soit encore : \(\lambda(1 - N) = 2 n e \cos r_N - 2 n e \cos r_1\)
si les angles restent faibles : \(\cos r \cong 1 - \frac{r^2}{2}\) et
\(2 n e (\cos r_N - \cos r_1) = 2 n e (\frac{r_1^2}{2} - \frac{r_N^2}{2})\) d'où \(\frac{r_N^2}{2} = \frac{\lambda(N-1)}{2 n e} + \frac{r_1^2}{2}\)
soit encore : \(r_N = \sqrt{\frac{\lambda(N-1)}{2 n e} + r_1^2}\)
Les anneaux sont donc d'autant plus serrés que l'épaisseur de la lame est grande.
Le rayon des anneaux augmente comme \(\sqrt{N-1}\)
les anneaux sont d'autant plus serrés que \(N\) augmente.
Complément :
Le cheminement des rayons lumineux à travers une lame mince d'épaisseur constante est visualisée dans l'animation suivante: