Particules pénétrant un champ magnétique
Partie
Question
Considérons des particules de charge \(q > 0\) qui pénètrent à la vitesse \(\vec v\) dans un champ magnétique \(\vec B\) constant et uniforme.
L'espace est rapporté à un référentiel orthonormé direct \((O ; x, y, z)\).
Sachant que \(\vec v\) est porté par l'axe des \(y\) et dirigé vers les \(y > 0\) et que \(\vec B\) est porté par l'axe des \(z\) et dirigé vers les \(z > 0\), calculer la force de Lorentz à laquelle sont soumises les particules.
Aide simple
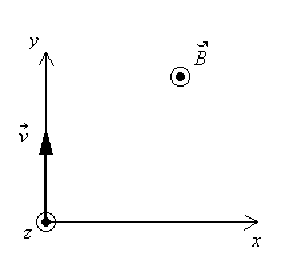
Exprimer \(q\vec v\) et \(\vec B\) dans la base \(\mathcal B=(\vec{e_x}, \vec{e_y}, \vec{e_z})\).
Rappel de cours
Le produit scalaire :
\(\vec A.\vec B=\left(\begin{array}{c} A_1\\A_2\\A_3\end{array} \right)_{\mathcal{B}} . \left(\begin{array}{c} B_1\\B_2\\B_3\end{array} \right)_{\mathcal{B}} =A_1B_1+A_2B_2+A_3B_3\)
Le produit vectoriel :
\(\vec{A}\wedge\vec{B}=\left(\begin{array}{c} A_1 \\ A_2 \\ A_3 \end{array}\right)_{\mathcal{B}}\wedge\left(\begin{array}{c} B_1 \\ B_2 \\ B_3 \end{array}\right)_{\mathcal{B}} =\left(\begin{array}{c} A_2B_3-A_3B_2 \\ A_3B_1-A_1B_3 \\ A_1B_2-A_2B_1 \end{array}\right)_{\mathcal{B}}\)
Les opérateurs vectoriels :
Système de repérage cartésien \(\mathcal{B}_{\mathrm{cart.}}(\vec{e_x}, \vec{e_y}, \vec{e_z})\)
gradient : \(\vec{\mathrm{grad}}U\) | divergence : \(\mathrm{div}\vec A\) | rotationnel : \(\vec{\mathrm{rot}}\vec A\) |
\(\left(\begin{array}{c} \displaystyle{ \frac{\partial U}{\partial x} } \\\\ \displaystyle{ \frac{\partial U}{\partial y} } \\\\ \displaystyle{ \frac{\partial U}{\partial z} } \end{array} \right)_{\mathcal{B}_{\mathrm{cart.}}}\) | \(\displaystyle{ \frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z} }\) | \(\left(\begin{array}{c} \displaystyle{ \frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z} } \\\\ \displaystyle{ \frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x} } \\\\ \displaystyle{ \frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y} }\end{array} \right)_{\mathcal{B}_{\mathrm{cart.}}}\) |
Système de repérage cylindrique \(\mathcal B_{\mathrm{cyl.}}(\vec{e_r},\vec{e_{\theta}},\vec{e_z})\)
gradient : \(\vec{\mathrm{grad}}U\) | divergence : \(\mathrm{div}\vec A\) | rotationnel : \(\vec{\mathrm{rot}}\vec A\) |
\(\left(\begin{array}{c} \displaystyle{ \frac{\partial U}{\partial r} } \\\\ \displaystyle{ \frac{1}{r} \frac{\partial U}{\partial \theta} } \\\\ \displaystyle{ \frac{\partial U}{\partial z} } \end{array} \right)_{\mathcal{B}_{\mathrm{cyl.}}}\) | \(\displaystyle{ \frac{1}{r} \frac{\partial (r . A_r) }{\partial r} + \frac{1}{r} \frac{\partial A_{\theta}}{\partial \theta}+\frac{\partial A_z}{\partial z} }\) | \(\left(\begin{array}{c} \displaystyle{ \frac{1}{r}\frac{\partial A_z}{\partial\theta}-\frac{\partial A_\theta}{\partial z} } \\\\ \displaystyle{ \frac{\partial A_r}{\partial z}-\frac{\partial A_z}{\partial r} } \\\\ \displaystyle{ \frac{1}{r} \left( \frac{\partial(r. A_{\theta})}{\partial r}-\frac{\partial A_r}{\partial \theta} \right)} \end{array} \right)_{\mathcal{B}_{\mathrm{cyl.}}}\) |
Nom de l'outil | Comment s'énonce-t-il ? | Quand l'utiliser ? |
Théorème d'Ampère | \(\displaystyle{ \oint_{\mathcal C}\vec B.\vec{\mathrm{d}l}=\mu_0\sum I }\) | Pour calculer \(\vec B\) si la géométrie du problème permet un calcul simple de la circulation de \(\vec B\). |
Loi de Biot et Savart | \(\displaystyle{ \vec B(M)=\frac{\mu_0}{4\pi}\int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\frac{\vec{PM}}{PM^3} }\) | Pour calculer \(\vec B\) si la géométrie de la distribution ne permet pas une application simple du théorème d'Ampère. |
Relation champ magnétostatique/ potentiel vecteur | \(\vec{B}(M)=\vec{\mathrm{rot}}\vec A(M)\) | Pour calculer \(\vec B\) si \(\vec A\) est connu. |
Définition de la force de Laplace | \(\vec{F_m}=\displaystyle{ \int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\vec B_{\mathrm{ext}}(P) }\) | Pour calculer la force qui s'exerce sur une distribution \(\mathcal D\) soumise à un champ magnétostatique extérieur \(\vec B_{\mathrm{ext}}\) |
Théorème de Maxwell | \(W_{2\leftarrow1}=I . \Phi_c\) | Pour calculer directement le torseur des forces qui agissent sur un circuit. |
Définition du potentiel vecteur | \(\displaystyle{ \vec A(M)=\int_{\mathcal D}\frac{\mu_0}{4\pi}\frac{\vec{\mathrm{d}\mathcal C}(P)}{PM} }\) | Pour calculer \(\vec A\) si la distribution a un haut degré de symétrie. |
Solution détaillée
La force de Lorentz est calculée à partir de l'expression : \(\vec F=q\vec v\wedge\vec B\).
Exprimons \(q\vec v\) et \(\vec B\) dans la base \(\mathcal B=(\vec{e_x}, \vec{e_y}, \vec{e_z})\) :
\(q \vec v=\left(\begin{array}{c} 0 \\ qv \\ 0 \end{array}\right) \quad \vec{B}=\left(\begin{array}{c} 0 \\ 0 \\ B \end{array}\right)\)
Cette force peut maintenant être calculée à partir du produit vectoriel :
\(\vec F = q\vec{v}\wedge\vec{B}=\left(\begin{array}{c} 0 \\ qv \\ 0 \end{array}\right)\wedge\left(\begin{array}{c} 0 \\ 0 \\ B \end{array}\right)=\left(\begin{array}{c} qv B \\ 0 \\ 0 \end{array}\right)=qvB.\vec{e_x}\)
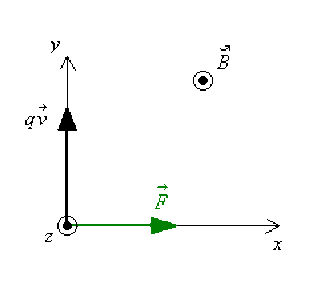
Les particules de charges positives sont donc déviées vers les \(x > 0\).