Théorème de Maxwell : déplacement d'une tige conductrice
Partie
Question
Une tige rigide conductrice rectiligne se déplace, sous l'action de la force de Laplace \(\vec F\), sur deux rails conducteurs parallèles distants de \(l\). Un générateur de courant d'intensité constante \(I\) est branché aux extrémités des deux rails. L'ensemble est placé dans un champ magnétostatique extérieur \(\vec B_{\mathrm{ext}}\) uniforme et perpendiculaire au plan des deux rails. L'espace est rapporté à un référentiel orthonormé direct \((O ; x, y, z)\).
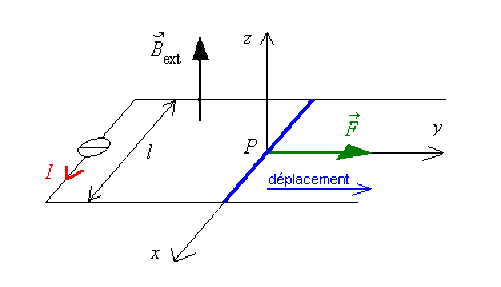
Déterminer la force de Laplace exercée sur la tige en utilisant le théorème de Maxwell.
Aide simple
Pour déterminer la force de Laplace, écrire le théorème de Maxwell :
exprimer le travail de cette force au cours du déplacement,
déterminer le produit du courant et du flux coupé par le champ magnétostatique au cours du déplacement,
identifier les deux expressions pour déterminer \(F\).
Rappel de cours
Le produit scalaire :
\(\vec A.\vec B=\left(\begin{array}{c} A_1\\A_2\\A_3\end{array} \right)_{\mathcal{B}} . \left(\begin{array}{c} B_1\\B_2\\B_3\end{array} \right)_{\mathcal{B}} =A_1B_1+A_2B_2+A_3B_3\)
Le produit vectoriel :
\(\vec A\wedge\vec B=\left(\begin{array}{c} A_1\\A_2\\A_3\end{array} \right)_{\mathcal{B}} \wedge\left(\begin{array}{c} B_1\\B_2\\B_3\end{array} \right)_{\mathcal{B}} =\left(\begin{array}{c} A_2B_3-A_3B_2\\A_3B_1-A_1B_3\\A_1B_2-A_2B_1\end{array} \right)_{\mathcal{B}}\)
Les opérateurs vectoriels :
Système de repérage cartésien \(\mathcal{B}_{\mathrm{cart.}}(\vec{e_x}, \vec{e_y}, \vec{e_z})\)
gradient : \(\vec{\mathrm{grad}}U\) | divergence : \(\mathrm{div}\vec A\) | rotationnel : \(\vec{\mathrm{rot}}\vec A\) |
\(\left(\begin{array}{c} \displaystyle{ \frac{\partial U}{\partial x} } \\ \displaystyle{ \frac{\partial U}{\partial y} } \\ \displaystyle{ \frac{\partial U}{\partial z} } \end{array} \right)_{\mathcal{B}_{\mathrm{cart.}}}\) | \(\displaystyle{ \frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z} }\) | \(\left(\begin{array}{c} \displaystyle{ \frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z} } \\ \displaystyle{ \frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x} } \\ \displaystyle{ \frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y} }\end{array} \right)_{\mathcal{B}_{\mathrm{cart.}}}\) |
Système de repérage cylindrique \(\mathcal B_{\mathrm{cyl.}}(\vec{e_r},\vec{e_{\theta}},\vec{e_z})\)
gradient : \(\vec{\mathrm{grad}}U\) | divergence : \(\mathrm{div}\vec A\) | rotationnel : \(\vec{\mathrm{rot}}\vec A\) |
\(\left(\begin{array}{c} \displaystyle{ \frac{\partial U}{\partial r} } \\ \displaystyle{ \frac{1}{r} \frac{\partial U}{\partial \theta} }\\ \displaystyle{ \frac{\partial U}{\partial z} } \end{array} \right)_{\mathcal{B}_{\mathrm{cyl.}}}\) | \(\displaystyle{ \frac{1}{r} \frac{\partial (r . A_r) }{\partial r} + \frac{1}{r} \frac{\partial A_{\theta}}{\partial \theta}+\frac{\partial A_z}{\partial z} }\) | \(\left(\begin{array}{c} \displaystyle{ \frac{1}{r} \frac{\partial A_z}{\partial \theta}-\frac{\partial A_ \theta}{\partial z} } \\ \displaystyle{ \frac{\partial A_r}{\partial z}-\frac{\partial A_z}{\partial r} } \\ \displaystyle{ \frac{1}{r} \left( \frac{\partial (r. A_{\theta})}{\partial r}-\frac{\partial A_r}{\partial \theta} \right)} \end{array} \right)_{\mathcal{B}_{\mathrm{cyl.}}}\) |
Nom de l'outil | Comment s'énonce-t-il ? | Quand l'utiliser ? |
Théorème d'Ampère | \(\displaystyle{ \oint_{\mathcal C}\vec B.\vec{\mathrm{d}l}=\mu_0\sum I }\) | Pour calculer \(\vec B\) si la géométrie du problème permet un calcul simple de la circulation de \(\vec B\). |
Loi de Biot et Savart | \(\displaystyle{ \vec B(M)=\frac{\mu_0}{4\pi}\int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\frac{\vec{PM}}{PM^3} }\) | Pour calculer \(\vec B\) si la géométrie de la distribution ne permet pas une application simple du théorème d'Ampère. |
Relation champ magnétostatique/ potentiel vecteur | \(\vec{B}(M)=\vec{\mathrm{rot}}\vec A(M)\) | Pour calculer \(\vec B\) si \(\vec A\) est connu. |
Définition de la force de Laplace | \(\vec{F_m}=\displaystyle{ \int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\vec B_{\mathrm{ext}}(P) }\) | Pour calculer la force qui s'exerce sur une distribution \(\mathcal D\) soumise à un champ magnétostatique extérieur \(\vec B_{\mathrm{ext}}\) |
Théorème de Maxwell | \(W_{2\leftarrow1}=I . \Phi_c\) | Pour calculer directement le torseur des forces qui agissent sur un circuit. |
Définition du potentiel vecteur | \(\displaystyle{ \vec A(M)=\int_{\mathcal D}\frac{\mu_0}{4\pi}\frac{\vec{\mathrm{d}\mathcal C}(P)}{PM} }\) | Pour calculer \(\vec A\) si la distribution a un haut degré de symétrie. |
Solution détaillée
La force de Laplace appliquée à une distribution de courant \(\mathcal{D}\) peut être déterminée à partir du théorème de Maxwell :
\(\mathrm{d}W = I . \mathrm{d} \Phi \quad\) avec \(\displaystyle{ \mathrm{d} \Phi = \int_{\mathcal{D}} \mathrm{d}^2 \Phi }\) , \(\mathrm{d}^2 \Phi = \vec B_{\mathrm{ext}} . \vec{ \mathrm{d} \mathcal{S}}\) et \(\vec{ \mathrm{d} \mathcal{S}} = \vec{\mathrm{d} l}_d \wedge \vec{\mathrm{d} l}(P)\)
\(\vec{\mathrm{d} l}_d\) correspond au déplacement élémentaire du conducteur sous l'action de la force de Laplace.
\(\vec{\mathrm{d} l}(P)\) est l'élément du conducteur centré en \(P\) et orienté suivant le sens du courant.
\(\mathrm{d} W = \vec F . \vec{\mathrm{d} l}_d\) représente le travail de la force de Laplace au cours d'un déplacement \(\vec{\mathrm{d} l}_d\).
Déterminons le travail de la force de Laplace.
Dans cet exercice, le déplacement et la force sont dirigés suivant l'axe des \(y\). À partir des vecteurs \(\vec F\) et \(\vec{\mathrm{d} l}_d\) exprimés dans la base \(\mathcal{B} = (\vec{e_x}, \vec{e_y}, \vec{e_z})\), nous obtenons :
\(\mathrm{d} W = \vec F . \vec{\mathrm{d} l}_d = \vec F . \vec{\mathrm{d} y} = \left( \begin{array}{c} 0 \\ F \\ 0 \end{array} \right) \cdot \left( \begin{array}{c} 0 \\ \mathrm{d} y \\ 0 \end{array} \right) = F . \mathrm{d} y\)
Nous devons ensuite exprimer le flux coupé par le champ magnétostatique \(\vec B_{\mathrm{ext}}\) au cours du déplacement \(\vec{\mathrm{d} l}_d\) de l'élément conducteur associé à l'élément \(\vec{\mathrm{d} l}(P)\) :
\(\mathrm{d}^2 \Phi = \vec B_{\mathrm{ext}} . \vec{ \mathrm{d} \mathcal{S}} \mathrm{ }\) avec \(\mathrm{ } \vec{ \mathrm{d} \mathcal{S}} = \vec{\mathrm{d} l}_d \wedge \vec{\mathrm{d} l}(P)\)
- Détermination de la surface balayée :
À partir des vecteurs \(\vec{\mathrm{d} l}_d\) (déplacement du conducteur suivant l'axe des \(y\) positifs) et \(\vec{\mathrm{d} l}(P)\) (dans le sens du courant, ici vers les \(x\) négatifs) exprimés dans la base \(\mathcal{B} = (\vec{e_x}, \vec{e_y}, \vec{e_z})\), nous obtenons :
\(\vec{ \mathrm{d} \mathcal{S}} = \vec{\mathrm{d} l}_d \wedge \vec{\mathrm{d} l}(P) = \left( \begin{array}{c} 0 \\ \mathrm{d} y \\ 0 \end{array} \right) \wedge \left( \begin{array}{c} - \mathrm{d}x \\ 0 \\ 0 \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \\ \mathrm{d} x . \mathrm{d} y \end{array} \right)\)
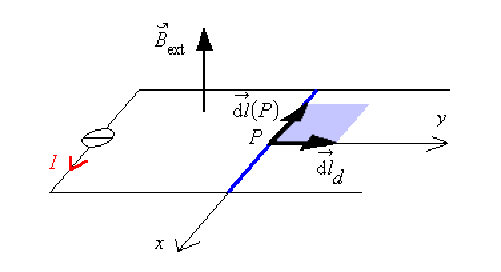
- Expression du flux coupé par le champ magnétostatique \(\vec B_{\mathrm{ext}}\) dans le déplacement \(\vec{\mathrm{d} l}_d\) de l'élément conducteur associé à l'élément de longueur \(\vec{\mathrm{d} l}(P)\) :
\(\mathrm{d}^2 \Phi = \vec B_{\mathrm{ext}} . \vec{ \mathrm{d} \mathcal{S}} = \left( \begin{array}{c} 0 \\ 0 \\ B_{\mathrm{ext}} \end{array} \right) \cdot \left( \begin{array}{c} 0 \\ 0 \\ \mathrm{d} x . \mathrm{d} y \end{array} \right) =B_{\mathrm{ext}} . \mathrm{d} x . \mathrm{d} y\)
- Expression du flux coupé par le champ magnétostatique \(\vec B_{\mathrm{ext}}\) dans le déplacement \(\vec{\mathrm{d} l}(P)\) du conducteur sur toute sa longueur \(l\) :
\(\displaystyle{ \mathrm{d} \Phi = \int_{\mathcal{D}} \mathrm{d}^2 \Phi = \int_0^l B_{\mathrm{ext}} . \mathrm{d} y . \mathrm{d} x = B_{\mathrm{ext}} . l . \mathrm{d} y}\)
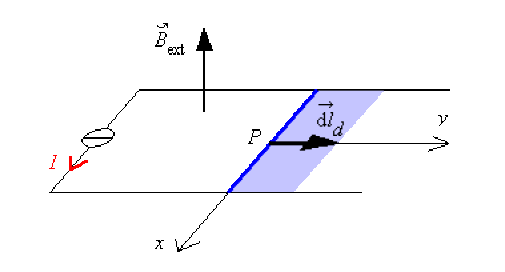
À partir du théorème de Maxwell, \(\mathrm{d} W = I . \mathrm{d} \Phi\), nous devons maintenant identifier chaque terme pour obtenir l'expression de la force de Laplace :
\(F . \mathrm{d} y = I . l . B_{\mathrm{ext}} . \mathrm{d} y\)
d'où après simplification : \(F = I . l . B_{\mathrm{ext}}\)