Cinématique dans l'espace-temps

La vitesse est définie par \(\vec v=\displaystyle\frac{ d\overrightarrow{ {OM}}}{ {dt}}\)

En utilisant la décomposition sur la base \((\vec i,\vec j,\vec k)\) : \(\vec v=\displaystyle\frac{ {d(x}\vec i )}{ {dt}}+\displaystyle\frac{ {d(y}\vec j )}{ {dt}}+\displaystyle\frac{ {d(z}\vec k )}{ {dt}}=\displaystyle\frac{ {dx}}{ {dt}}\vec i+ x\displaystyle\frac{ d\vec i}{ {dt}}+......\)

Or la base \((\vec i,\vec j,\vec k)\) est fixe dans le repère, par suite : \(\displaystyle\frac{ d\vec i}{ {dt}}=\vec0\) \(\displaystyle\frac{ d\vec j}{ {dt}}=\vec0\) \(\displaystyle\frac{ d\vec k}{ {dt}}=\vec0\)

\(\vec v=\displaystyle\frac{ {dx}}{ {dt}}\vec i+\displaystyle\frac{ {dy}}{ {dt}}\vec j+\displaystyle\frac{ {dz}}{ {dt}}\vec k\)

On notera souvent : \(\vec v= x'\vec i+ y'\vec j+ z'\vec k\)

On voit ainsi que le calcul de la dérivée d'une fonction vectorielle de la variable scalaire temps se ramène au calcul des dérivées par rapport au temps des composantes du vecteur; les composantes sont des fonctions scalaires d'une variable scalaire.

L'accélération est définie par \(\vec y=\displaystyle\frac{ d\vec v}{ {dt}}\)

En utilisant la décomposition du vecteur vitesse sur la base cartésienne, il en résulte avec le même raisonnement que ci-dessus : \(\vec y=\displaystyle\frac{ d^2 x}{ {dt}^2}\vec i+\displaystyle\frac{ d^2 y}{ {dt}^2}\vec j+\displaystyle\frac{ d^2 z}{ {dt}^2}\vec k\)

On écrira aussi : \(\vec y= {x''}\vec i+ {y''}\vec j+ {z''}\vec k\)

On exprime \(\overrightarrow {OM}\) à l'aide de sa décomposition sur la base polaire cylindrique et on dérive par rapport au temps : \(\vec v=\displaystyle\frac{ d\rho}{ {dt}}\overrightarrow{ u_\rho}+\rho\displaystyle\frac{ d\overrightarrow{ u_\rho}}{ {dt}}+\displaystyle\frac{ {dz}}{ {dt}}\vec k+ z\displaystyle\frac{ d\vec k}{ {dt}}\)

\(\vec k\) est un vecteur fixe du repère (indépendant du temps), mais \(\overrightarrow{ u_\rho}\) bien que de norme constante, a une direction associée à la position du mobile \(M\) et dépend du temps. Il faut donc exprimer la dérivée de \(\overrightarrow{ u_\rho}\) par rapport au temps :

\(\displaystyle\frac{d\overrightarrow{ u_\rho}} {dt}=\displaystyle\frac{d\overrightarrow{ u_\rho}}{ d\Phi}\displaystyle\frac{ d\Phi} {dt}\)

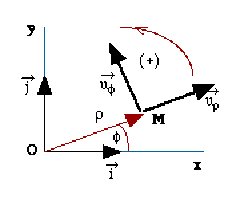
A partir de la définition du vecteur position et du résultat sur la dérivation par rapport à un paramètre de rotation d'un vecteur, il vient : \(\displaystyle\frac{d\overrightarrow{ u_\rho}}{ d\Phi}=\overrightarrow{ u_\Phi}\)

En reportant dans l'expression de la vitesse : \(\vec v=\displaystyle\frac{ d\rho}{ {dt}}\overrightarrow{ u_\rho}+\rho\displaystyle\frac{ d\Phi}{ {dt}}\overrightarrow{ u_\Phi}+\displaystyle\frac{ {dz}}{ {dt}}\vec k\) noté \(\vec v=\rho'\overrightarrow{ u_\rho}+\rho\Phi'\overrightarrow{ u_\Phi}+ z'\vec k\)

On part à nouveau de \(\vec\gamma=\frac{dv}{dt}=\frac{d^2\rho}{{dt}^2}\vec{u_\rho}+\frac{d\rho}{dt}\frac{d\rho}{dt}+\frac{d\rho}{dt}\frac{d\Phi}{dt}\vec{u_\Phi}+\rho\frac{d^2\Phi}{{dt}^2}\vec{ u_\Phi}+\rho\frac{d\Phi}{dt}\frac{d\vec{u_\Phi}}{dt}+\frac{d^2z}{{dt}^2}\vec k\)

Pour calculer la dérivée de \(\vec{ u_\Phi}\) par rapport au temps, \(\displaystyle\frac{ d\vec{ u_\Phi}} {dt}=\displaystyle\frac{ d\vec{ u_\Phi}}{ d\Phi}\displaystyle\frac{ d\Phi} {dt}\)

on peut appliquer le résultat général : la dérivée par rapport à une variable de rotation d'un vecteur unitaire est le vecteur unitaire ayant subi une rotation de \(+1/2\):

Par suite : \(\displaystyle\frac{ d\overrightarrow{ u_\phi}}{ d\phi}=-\overrightarrow{ u_\rho}\) et \(\vec\gamma=\bigg(\displaystyle\frac{ d^2\rho}{ {dt}^2}-\rho\bigg(\displaystyle\frac{ d\phi} {dt}\bigg)^2\bigg)\overrightarrow{ u_{\rho}}+\bigg(2\displaystyle\frac{ d\rho} {dt}\displaystyle\frac{ d\phi} {dt}+\rho\displaystyle\frac{ d^2\phi}{ {dt}^2}\bigg)\overrightarrow{ u_\phi}+\displaystyle\frac{ d^2 z}{ {dt}^2}\vec k\)

\(\vec\gamma=(\rho''-\rho\phi^2)\overrightarrow{ u_\rho}+(2\rho'\phi'+\rho\phi'')\overrightarrow{ u_\phi}+ z''\vec k\)

La notation \(\rho''\) et \(\phi''\) indique qu'il s'agit de la dérivée seconde par rapport au temps.

Le calcul de la vitesse conduit à l'expression \(\vec v= r'\vec{ u_ r}+ r\theta' \vec{ u_\theta}+ r\sin\theta\phi' \vec{ u_\phi}\)

Les composantes de l'accélération sont développées ci-dessous :

• \(\vec\gamma\cdot\vec{ u_ r}=\gamma r= r''- r(\theta'^2+\sin^2\theta\phi'^2)\)

• \(\vec\gamma\cdot\vec{ u_\theta}=\gamma\theta=\displaystyle\frac{1} r\displaystyle\frac{ d( r^2\theta')}{ {dt}}- r\sin\theta\cos\theta\phi'^2\)

• \(\vec\gamma\cdot\vec{ u_\phi}=\gamma\phi=\displaystyle\frac1{( r\sin\theta)}\displaystyle\frac d{ {dt}}( r^2\sin^2\theta\phi')\)