Cinématique dans l'espace-temps

Soit une trajectoire circulaire de centre \(O\) dont le plan n'est pas fixe au cours du temps.

A tout mobile \(M\), animé sur cette trajectoire d'une vitesse \(\vec {v(} {t)}\) dans un référentiel \(R( O,\vec i,\vec j,\vec k)\), on peut associer un vecteur vitesse instantanée de rotation \(\overrightarrow{\Omega {(t)}}\) défini par la relation suivante : \(\vec v=\vec\Omega\land\overrightarrow{ {OM}}\) où le trièdre \((\vec v,\vec\Omega,\overrightarrow{ {OM}})\) est direct.

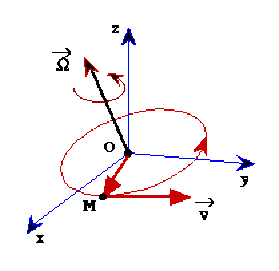
La simulation suivante montre les rotations élémentaires autour de chacun des trois axes de coordonnées.

Dans la plupart des cas étudiés, seule la rotation par rapport à un axe intervient. Mais par exemple, lors du mouvement d'un point d'une toupie, la direction et la grandeur de \(\vec\Omega\) changent à chaque instant, il faut alors tenir compte du cas général des trois rotations par rapport aux axes de référence.

• La trajectoire est circulaire de rayon \(R\)

  Compte tenu de la symétrie de ce mouvement, il est commode d'utiliser les coordonnées polaires planes.

  • La vitesse est donnée à partir de l'expression \(\vec v=\displaystyle\frac{ d\rho} {dt}\vec{ u_\rho}+\rho\displaystyle\frac{ d\vec{ u_\rho}} {dt}\) sachant que \(\rho = R = cte\) et que \(\vec v= R\phi'\vec{ u_\phi}\)

  • Le vecteur vitesse instantanée de rotation est tel que : \(R\phi'\vec{ u_\phi}=\vec\Omega\land R\vec{ u_\rho}\)

    Soit : \(\vec\Omega=\phi'\vec k\). Sa norme \(||\vec\Omega||=\phi'\) est appelée vitesse angulaire

  • L'accélération est donnée par l'expression \(\vec\gamma=(\rho''-\rho\phi'^2)\vec{ u_\rho}+(2\rho'\phi'+\rho\phi'')\vec{u_\phi}\) sachant que \(\rho = R = cte\) : \(\vec\gamma=- R\phi'^2\vec{ u_\rho}+ R+ R\phi''\vec{ u_\phi}=- R\Omega^2\vec{ u_\rho}+ R\Omega'\vec{ u_\phi}\)

    Pour ce mouvement, la base de Frenet est liée à la base locale : \(\tau=\vec{ u_\phi}\) et \(\vec n=-\vec{ u_\rho}\)

    L'accélération tangentielle est : \(\vec{\gamma\tau}= R\Omega'\vec{u_\phi}\)

    L'accélération normale : \(\vec{\gamma n}=- R\Omega^2\vec{ u_\rho}\)

    L'accélération normale est centripète (dirigée vers le centre du cercle), elle est liée à la courbure de la trajectoire

• Le mouvement est circulaire uniforme :

  La vitesse horaire est constante, le vecteur vitesse est \(\vec v= R\Omega\vec{ u_\phi}\),la vitesse horaire est donc \(v = R\Omega\) (norme du vecteur vitesse); par suite, la vitesse angulaire est constante ainsi que le vecteur vitesse instantanée de rotation \(\vec\Omega\).

  L'accélération tangentielle est nulle et l'accélération normale de norme constante.

  Le temps mis pour faire un tour s'appelle la période \(T\), elle se mesure en seconde \((s)\).

  L'inverse de la période s'appelle la fréquence \(n\); elle mesure le nombre de tours effectués par unité de temps. Elle s'exprime en Hertz (Hz) : \(T=\displaystyle\frac1 v=\displaystyle\frac{2\pi}\Omega\)

\(\Omega\) est le rapport de la mesure d'un angle et d'un temps. \(\Omega\) s'exprime en radian par seconde (\(rad/s\) ou \(rad.s^{-1}\))