Notion de système de points matériels
Système mécanique
Un système mécanique est un sous-ensemble de l'ensemble des éléments de l'espace (points matériels) constitué des points matériels appartenant au système que l'on désire étudier.
- Les éléments appartenant à ce sous-ensemble sont les éléments intérieurs au système.
- Les éléments n'appartenant pas à ce sous-ensemble sont extérieurs au système.
Le choix du système dépend essentiellement du type de problème étudié il faut faire le choix qui permet la plus grande simplicité d'expression des lois de la mécanique.
Exemple
Pour étudier un système, on doit définir sa limite (ce qui en fait partie et ce qui n'en fait pas partie), pour pouvoir remplacer l'extérieur au système (tout ce qui n'en fait pas partie) par l'ensemble des forces qui représentent l'action sur ce système de l'extérieur au système.
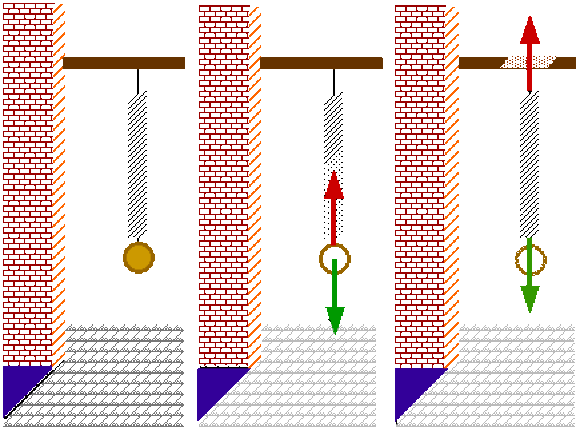
Tout corps est soumis à un ensemble de forces qui représentent l'action de son environnement.
En particulier, s'il est doté d'une masse \(m\), il est soumis à son poids.
Dans l'exemple ci-dessus, le système considéré est une masse fixée à un ressort : on devra considérer son poids ainsi que la force de rappel qu'exerce le ressort sur cette masse.
Si le système est constitué de plusieurs points matériels de masse \(m_i\), la masse du système est \(\displaystyle{\displaystyle{\sum_{i=1}^N}m_i}\)
Si le système est indéformable, c'est à dire si les distances entre les points sont invariantes c'est un solide.
Si les points constituant le système sont mobiles les uns par rapport aux autres, le système est déformable.
Dans certains cas, le système, bien que de dimensions finies non nulles, pourra être assimilé à un point matériel unique, sa masse est alors notée \(m\). L'assimilation ne peut être faite que si l'ensemble est indéformable.
On admet, en Mécanique classique, le principe de conservation de la masse : la masse, à l'instant \(t\), de tout système matériel est indépendante de \(t\).
Centre de masse d'un système de points matériels
Soit un système matériel constitué de \(N\) points matériels \(M_i\) de masse \(m_i\) , de coordonnées \(x_i , y_i , z_i\) et un point \(O\) quelconque.
On appelle centre de masse du système matériel de masse totale \(m\), le point \(G\) tel que:
\(\displaystyle{\sum_{i=1}^Nm_i\overrightarrow{GM_i}=\overrightarrow0}\)
Le centre de masse est aussi appelé centre d'inertie.
Dans le champ de pesanteur, localement uniforme, le centre de masse est confondu avec le centre de gravité.
Si \(O\) est un point quelconque pris pour origine on peut écrire :
\(\displaystyle{\sum_{i=1}^Nm_i(\overrightarrow{GO}+\overrightarrow{OM_i})=\overrightarrow{GO}\sum_{i=1}^Nm_i+\sum_{i=1}^Nm_i\overrightarrow{OM_i}=\overrightarrow0}\)
ou
\(\displaystyle{\sum_{i=1}^Nm_i\overrightarrow{OM_i}=\overrightarrow{OG}\sum_{i=1}^Nm_i=m\overrightarrow{OG}}\)
\(\displaystyle{\overrightarrow{OG}=\frac{1}{m}\sum_{i=1}^Nm_i\overrightarrow{OM_i}}\)
Si \(O\) est l'origine d'un repère \(O_{xyz}\), les coordonnées de \(G\) sont :
\(\displaystyle{X_G=\frac{1}{m}\sum_{i=1}^Nm_ix_i\quad Y_G=\frac{1}{m}\sum_{i=1}^Nm_iy_i\quad Z_G=\frac{1}{m}\sum_{i=1}^Nm_iz_i}\)
Remarques:
Dans le modèle du point matériel, le centre de masse n'est pas, en général, un point matériel du système.
Si le système est indéformable, le centre de masse occupe une position fixe par rapport à l'ensemble des points du système; si le système est déformable, sa position n'est pas fixe.