Télescope (3)
Durée : 5 mn
Note maximale : 2
Question
Etude d'un télescope(suite) : on veut de plus que l'image finale soit en \(S\) (on pourra ainsi y placer une plaque photo) et que le grandissement donné par \(M'\) soit \(k\), avec \(k > 0\) connu.
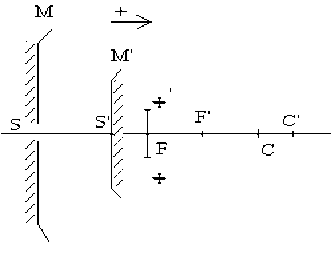
Trouver le rayon \(R'\) de \(M'\) et sa position par rapport à \(M\) ( en calculant \(SS'\)).
Solution
\(A'=S\) et : \(\gamma=-\frac{\overline{S'A'}}{\overline{S'F}}=k=-\frac{\overline{S'S}}{\overline{S'F}}\) d'où \(\overline{S'S}=-k\cdot\overline{S'F}=-k\cdot(\overline{S'S}+\overline{SF})\)
\(\overline{S'S}(1+k)=-k\cdot\overline{SF}\) or \(\overline{SF}>0\) et \(SF=\frac R2\) ce qui entraine : \(\overline{S'S}=-\frac k{k+1}\cdot\frac R2\)
la formule de position conduit à : \(\frac1{\overline{S'S}}+\frac1{\overline{S'F}}=\frac1{\overline{S'F'}}=\frac2{\overline{S'C'}}=\frac2{R'}\)
où \(\overline{S'S}=-\frac k{k+1}\cdot\frac R2\)
\(\overline{S'F}=\overline{S'S}+\overline{SF}=-\frac k{k+1}\cdot\frac R2+\frac R2=\frac R2\left(-\frac k{k+1}+1\right)=\frac1{k+1}\cdot\frac R2\)
d'où \(\frac{2(k+1)}{-k.R}+\frac{2(k+1)}R=\frac2{R'}\)
\(\frac{2(k+1)}R\left(1-\frac1k\right)=\frac2{R'}\)
et enfin : \(R'=\frac k{k^2-1}\cdot R\)