Foyer objet [Dioptre Sphérique]

Foyer objet

Approximation de Gauss^[1] :

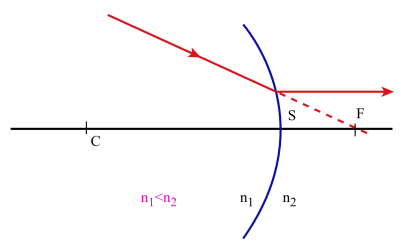
Si l'on définit le foyer objet^[2] F comme étant le point de l'axe dont l'image^[3] est située à l'infini sur l'axe on pourra considérer que CA₂ et SA₂ sont peu différents et la relation :

\(\mathrm n_1~\frac{\overline{\mathrm{CA}_1}}{\overline{\mathrm{SA}_1}}=\mathrm n_2~\frac{\overline{\mathrm{CA}_2}}{\overline{\mathrm{SA}_2}}~~\)

peut s'écrire : \(\frac{\overline{\mathrm{SF}}}{\overline{\mathrm{CF}}}=\frac{\mathrm n_1}{\mathrm n_2}\)

soit encore : \(\overline{\mathrm{SF}}=-\overline{\mathrm{CS}}~\frac{\mathrm n_1}{\mathrm n_1~-~\mathrm n_2}\)

cette quantité notée f est la distance focale objet du dioptre sphérique.

Dans le cas du dioptre concave : \(\overline{\mathrm{CS}}>0\)

si \(\mathrm n_1\) < \(\mathrm n_2\), F' est virtuel
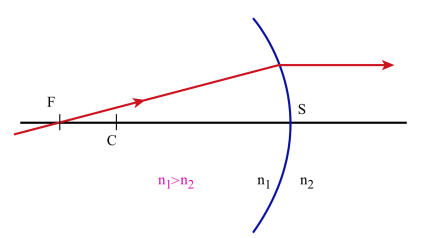
si \(\mathrm n_1\) > \(\mathrm n_2\), F' est réel

Un rayon incident passant par le foyer objet du dioptre se réfractera en un rayon parallèle à l'axe optique du dioptre.

On a d'autre part :

\(\overline{\mathrm{CF}}=\overline{\mathrm{CS}}~+~\overline{\mathrm{SF}}=\frac{\mathrm n_2}{\mathrm n_1~-~\mathrm n_2}\overline{\mathrm{CS}}=-\overline{\mathrm{SF'}}\)

\(\overline{\mathrm{CF'}}=\overline{\mathrm{CS}}~+~\overline{\mathrm{SF'}}=\frac{\mathrm n_1}{\mathrm n_1~-~\mathrm n_2}\overline{\mathrm{CS}}=-\overline{\mathrm{SF}}\)

On constate alors que les foyers image et objet du dioptre sont symétriques par rapport au milieu de CS.

Notes

Conditions de GAUSS
Un système est utilisé dans les conditions de Gauss, lorsque les rayons qui le traversent sont peu inclinés sur l'axe principal ( rayons paraxiaux).
On peut alors considérer valable l'approximation qui permet de confondre l'angle d'incidence et son sinus (a~sina).
Dans ces conditions, il y a stigmatisme pour les points objet et image.
Ce stigmatisme est dit approché car il nécessite les conditions de Gauss pour être réalisé.
C'est en 1841 que Gauss a, le premier, présenté un exposé sur la formation des images dans cette approximation. Depuis, on emploie également les termes d'approximation de Gauss ou d'optique Gaussienne.
Foyers
Un foyer image est le point où convergent, après traversée du système optique, les rayons d'un faisceau parallèle. Il est dit principal sur l'axe principal, et secondaire en dehors de cet axe.
Un foyer objet est le point d'où partent les rayons qui, après traversée du système optique, forment un faisceau parallèle. Il est dit principal sur l'axe principal, et secondaire en dehors de cet axe.
Dans l'approximation des lentilles minces, l'ensemble des foyers secondaires et le foyer principal sont tous situés dans un plan de front appelé plan focal.
Image
On appelle image d'un objet par un système optique, l'ensemble des images des points de l'objet.
On appelle image d'un point, la zone de convergence des rayons, après traversée du système optique (image réelle) ou la zone d'où les rayons semblent provenir (image virtuelle). Lorsque cette zone se réduit à un point, le système est dit stigmatique.
En pratique, l'image ressemble à l'objet (sinon le système ne présente pas d'intérêt), elle peut être
- agrandie : plus grande que l'objet ( |grandissement| >1) ;
- rapetissée : plus petite que l'objet ( |grandissement| <1) ;
- droite : dans le même sens que l'objet (grandissement >0) ;
- renversée : dans le sens contraire à l'objet (grandissement <0) ;
- déformée : un système qui déforme parce qu'il n'a pas le même grandissement dans différentes directions provoque une anamorphose (ex : glace déformante) ;
- floue