Association de deux lentilles minces non accolées [Lentilles minces]

Association de deux lentilles minces non accolées

Association de deux Doublet

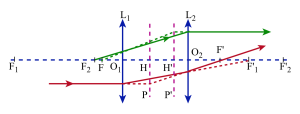
Deux lentilles minces^[1] \(L_1\) et \(L_2\) de distances focales^[2] \(f'_1\) et \(f'_2\) séparées par : \(e=\overline{O_{\mathit1}O_{\mathit2}}\) forment un doublet que l'on définit en général par son symbole, ensemble de 3 nombres algébriques m, n et p, généralement entiers et tels que :

\(\frac{f'_{\mathit1}}m=\frac en=\frac{f'_{\mathit2}}p\)

si l'on applique la formule de Gullstrand^[3] à cette association :

\(H'_1\) est en \(O_1\) et \(H_2\) est en \(O_2\) donc : \(\overline{H'_{\mathit1}H_{\mathit2}}=e\) et la convergence de l'association des deux lentilles est donnée par :

\(C=C_{\mathit1}~+~C_{\mathit2}~-~e.C_{\mathit1}.C_{\mathit2}=\frac1{f'_{\mathit1}}~+~\frac1{f'_{\mathit2}}~-~\frac{e}{f'_{\mathit1}.f'_{\mathit2}}=\frac{f'_{\mathit1}~+~f'_{\mathit2}~-~e}{f'_{\mathit1}.f'_{\mathit2}}=\frac1{f'}\) où f ' est la distance focale du doublet.

Posons : \(\overline{F'_{\mathit1}F_{\mathit2}}=\Delta\)

\(\Delta=\overline{F'_{\mathit1}O_{\mathit1}}~+~\overline{O_{\mathit1}O_{\mathit2}}~+~\overline{O_{\mathit2}F_{\mathit2}}=-f'_{\mathit1}~+~e~-~f'_{\mathit2}\) et donc : \(\frac1{f'}=-\frac{\Delta}{f'_{\mathit1}.f'_{\mathit2}}\) soit :

\(f'=-\frac{f'_{\mathit1}.f'_{\mathit2}}{\Delta}\)

le foyer image^[4] F ' du doublet est le conjugué de \(F'_1\) dans \(L_2\) :

\(\overline{F_{\mathit2}{F'}_{\mathit1}}~.~\overline{{F'}_{\mathit2}F'}={-f'}_{\mathit2}^2\) d'où :

\(\overline{{F'}_{\mathit2}F'}=\frac{{f'}_{\mathit2}^2}{\Delta}\)

De même, le foyer objet^[4] F est le conjugué de \(F_2\) dans \(L_1\) :

\(\overline{F_{\mathit1}F}~.~\overline{{F'}_{\mathit1}F_{\mathit2}}={-f'}_{\mathit1}^2\) d'où :

\(\overline{F_{\mathit1}F}=\frac{{f'}_{\mathit1}^2}{\Delta}\)

Tous les éléments cardinaux peuvent alors être mis en place.

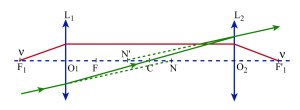
Doublet symétrique

Les doublets sont souvent symétriques et admettent le milieu C de \(O_1O_2\) comme centre de symétrie. Les points nodaux objet N et image N' sont les conjugués^[5] de C à travers \(L_1\) et \(L_2\) respectivement. Les points antinodaux sont les foyers \(F_1\) et \(F'_2\). Le foyer objet F du doublet est le milieu du segment \(NF_1\).

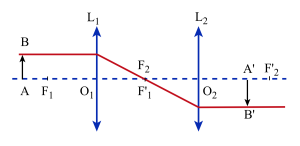
Doublet afocal

Un doublet est afocal si l'image^[6] d'un objet^[7] à l'infini est également à l'infini. Les foyers \(F'_1\) et \(F_2\) sont confondus. Nous prendrons les foyers \(F_1\) et \(F'_2\) qui sont conjugués, comme origines pour fixer la position de l'objet AB et celle de son image A'B'.Un doublet est afocal si l'image d'un objet à l'infini est également à l'infini. Les foyers \(F'_1\) et \(F_2\) sont confondus. Nous prendrons les foyers \(F_1\) et \(F'_2\) qui sont conjugués, comme origines pour fixer la position de l'objet AB et celle de son image A'B'.

Si l'on pose : \(~\overline{F'_{\mathit2}A'}=x'~\) et \(~\overline{F_{\mathit1}A}=x\) la relation donnant le grandissement^[8] axial s'écrit :

\(g=\gamma^2=\frac{x'}{x}=\Big(\frac{\overline{A'B'}}{\overline{AB}}\Big)^2=\Big(\frac{f'_{\mathit2}}{f'_{\mathit1}}\Big)^2\) soit :

\(\frac{x'}{x}=\Big(\frac{f'_{\mathit2}}{f'_{\mathit1}}\Big)^2\)

Notes

Lentille mince
Une lentille dont l'épaisseur au centre optique est négligeable devant les rayons de courbure des dioptres qui la limitent est dite mince. Dans le cas contraire c'est une lentille épaisse.
Approximation des lentilles minces
Une lentille mince peut être représentée par une lentille infiniment mince lorsqu'on étudie ses propriétés pour des distances [lentille-objet] ou [lentille-image] grandes devant l'épaisseur de la lentille. C'est ce qui est fait dans le cadre de l'optique géométrique élémentaire et en particulier dans l'atelier-schéma.
Distance focale d'une lentille
C'est la mesure algébrique de OF' où O est le centre optique et F' le foyer principal image.
Elle est positive pour une lentille convergente.
Puissance intrinseque (ou vergence) d'une lentille
C'est l'inverse de la distance focale exprimée en mètres, elle s'exprime en dioptries.
La puissance intrinseque d'une loupe de (distance) focale 5 cm est de 20 dioptries.
Formule de Gullstrand
Chacun des deux systèmes sera caractérisé par :
- ses foyers objet et image \(F_{\mathit1}\) et \(F'_{\mathit1}\) pour le premier système, \(F_{\mathit2}\) et \(F'_{\mathit2}\) pour le deuxième système.
- ses points principaux objet et image : \(H_{\mathit1}\) et \(H'_{\mathit1}\) pour le premier, \(H_{\mathit2}\) et \(H'_{\mathit2}\) pour le deuxième.
- ses distances focales objet et image : \(f_1=\overline{H_{\mathit1}F_{\mathit1}}\) et \(f'_1=\overline{H'_{\mathit1}F'_{\mathit1}}\) pour le premier, et \(f_2=\overline{H_{\mathit2}F_{\mathit2}}\) et \(f'_2=\overline{H'_{\mathit2}F'_{\mathit2}}\) pour le deuxième.
Le premier système sépare les milieux d'indice \(n_{\mathit1}\) et \(n\) tandis que le deuxième sépare les milieux d'indice \(n\) et \(n_2\).
L'ensemble des deux systèmes est caractérisé par une distance définie par : \(\overline{F_{\mathit1}F}~.~\overline{F'_{\mathit1}F_{\mathit2}}=f_{\mathit1}~.~f'_{\mathit1}\) que l'on appelle intervalle optique.
Détermination de la vergence de l'ensemble des deux systèmes :
Les vergences de chacun des systèmes sont données par :
\(C_{\mathit1}=-\frac{n_{\mathit1}}{f_{\mathit1}}=\frac{n}{f'_{\mathit1}}\)
\(C_{\mathit2}=-\frac{n}{f_{\mathit2}}=\frac{n_{\mathit1}}{f'_{\mathit2}}\)
tandis que la vergence de l'ensemble des deux systèmes est donnée par la formule de Gullstrand :
\(C=C_{\mathit1}~+~C_{\mathit2}~-~\frac{\overline{H'_{\mathit1}H_{\mathit2}}}n~C_{\mathit1}.C_{\mathit2}\)
Foyers
Un foyer image est le point où convergent, après traversée du système optique, les rayons d'un faisceau parallèle. Il est dit principal sur l'axe principal, et secondaire en dehors de cet axe.
Un foyer objet est le point d'où partent les rayons qui, après traversée du système optique, forment un faisceau parallèle. Il est dit principal sur l'axe principal, et secondaire en dehors de cet axe.
Dans l'approximation des lentilles minces, l'ensemble des foyers secondaires et le foyer principal sont tous situés dans un plan de front appelé plan focal.
Conjugués
Les points A et A' sont dits conjugués, par un système optique, lorsque A' est l'image de A. Le système est alors stigmatique pour les points A et A'.
Les plans P et P' sont dits conjugués, lorsque tout point du plan P possède une image dans le plan P'.
Image
On appelle image d'un objet par un système optique, l'ensemble des images des points de l'objet.
On appelle image d'un point, la zone de convergence des rayons, après traversée du système optique (image réelle) ou la zone d'où les rayons semblent provenir (image virtuelle). Lorsque cette zone se réduit à un point, le système est dit stigmatique.
En pratique, l'image ressemble à l'objet (sinon le système ne présente pas d'intérêt), elle peut être
- agrandie : plus grande que l'objet ( |grandissement| >1) ;
- rapetissée : plus petite que l'objet ( |grandissement| <1) ;
- droite : dans le même sens que l'objet (grandissement >0) ;
- renversée : dans le sens contraire à l'objet (grandissement <0) ;
- déformée : un système qui déforme parce qu'il n'a pas le même grandissement dans différentes directions provoque une anamorphose (ex : glace déformante) ;
- floue
Objet
En optique, on appelle objet tout ensemble de points lumineux. Il peut s'agir d'une source primaire qui produit de la lumière (ex : soleil, étoiles, filament de lampe allumée, écran de télévision ou d'ordinateur en fonction), ou d'une source secondaire qui diffuse une partie de la lumière qu'elle reçoit (ex : lune, planètes, la plupart des objets qui nous entourent lorsqu'ils sont éclairés).
On considère, en général, des objets plans situés dans des plans de front de systèmes optiques.
Dans des systèmes composés on pourra considérer qu'une image produite par une première partie du système est un objet pour le reste du système.
Grandissement
Le grandissement est un nombre algébrique, rapport entre les dimensions de l'image \(A'B'\) et de l'objet \(AB\) :
\(\gamma=\frac{\overline{A'B'}}{\overline{AB}}\)
Lorsque le système est aplanétique, l'image \(A'B'\) d'un objet \(AB\) situé dans un plan de front est également dans un plan de front. Le grandissement mesuré dans ces conditions est un grandissement transverse.
Le grandissement longitudinal (ou axial) est le rapport algébrique des dimensions de l'image et de l'objet prises suivant l'axe principal du système optique.
Le grandissement, parfois appelé grandissement linéaire ne doit pas être confondu avec le grossissement \(G\) qui fait référence à des angles.