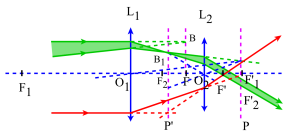
Oculaire négatif d'Huyghens
Son symbole est 3, 2, 1 : \(\frac{f'_{\mathit1}}3=\frac e2=\frac{f'_{\mathit2}}1=a\)
On voit que : \(~\overline{F'_{\mathit1}F_{\mathit2}}=\Delta=-2a~\) et en utilisant les relations :
\(\overline{F_{\mathit1}F}=-\frac{{f'}_{\mathit1}^2}{\Delta}~~\) \(~~f'=-\frac{f'_{\mathit1}~.~f'_{\mathit2}}{\Delta}~~\) et \(~~\overline{F'_{\mathit2}F'}=\frac{{f'}_{\mathit2}^2}{\Delta}\)
on en déduit : \(f'=\frac{3a}2~~\) \(~~\overline{F_{\mathit1}F}=\frac{9a}2~~\) \(~~\overline{F'_{\mathit2}F'}=-\frac a2~~\) et que \(F\) est au milieu de \(F_{\mathit2}O_{\mathit2}\) et \(F'\) au milieu de \(O_{\mathit2}F'_{\mathit2}\).
Quant aux plans principaux :
\(\overline{P'F'}=f'~~\) \(P'\) est en \(F_2\)
\(\overline{PF}=-f'~~\) \(P\) est en \(F'_2\)
F' est réel et l'oculaire est convergent[1] ; il est dit négatif car le foyer objet[2] est virtuel.
Cet oculaire ne pourra être utilisé que pour l'observation d'objets virtuels constitués par les images réelles fournies par un système optique[3] tel un objectif et dont l'interposition de l'oculaire empêche la formation de cette image réelle[4].
La puissance est : \(~P=\frac1{f'}=\frac2{3a}=\frac2{f'_{\mathit1}}\)
La puissance est double de celle qui serait obtenue en utilisant la première lentille comme loupe.
Cet oculaire satisfait de plus la condition d'achromatisme apparent : \(f'_{\mathit1}~+~f'_{\mathit2}=2e\)
Sur la figure est représentée la marche d'un faisceau lumineux[1] qui passerait par un point B du plan focal objet.