Double produit vectoriel de trois vecteurs
Définitions
On appelle double produit vectoriel entre trois vecteurs \(\overrightarrow{U}\), \(\overrightarrow{V}\) et \(\overrightarrow{W}\) le vecteur \(\overrightarrow{D}\) ou \(\overrightarrow{D'}\) défini par :
\(\overrightarrow{D} = \overrightarrow{U} \wedge \Big(\overrightarrow{V} \wedge \overrightarrow{W} \Big)= \Big(\overrightarrow{U} \cdot \overrightarrow{W}\Big)\overrightarrow{V} - \Big(\overrightarrow{U} \cdot \overrightarrow{V}\Big)\overrightarrow{W}\)
ou \(\overrightarrow{D'} = \Big(\overrightarrow{U} \wedge \overrightarrow{V} \Big)\wedge \overrightarrow{W} = \Big(\overrightarrow{U} \cdot \overrightarrow{W}\Big)\overrightarrow{V} - \Big(\overrightarrow{V} \cdot \overrightarrow{W}\Big)\overrightarrow{U}\)
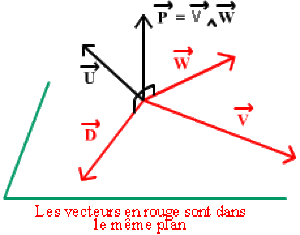
Le produit vectoriel \(\overrightarrow{p} = \overrightarrow{V} \wedge \overrightarrow{W}\) est représenté par un vecteur perpendiculaire au plan défini par \(\overrightarrow{V}\) et \(\overrightarrow{W}\). Le vecteur \(\overrightarrow{D} = \overrightarrow{U} \wedge \overrightarrow{p}\) perpendiculaire à \(\overrightarrow{p}\) se trouve dans le plan des vecteurs \(\overrightarrow{V}\) et \(\overrightarrow{W}\). Le vecteur \(\overrightarrow{D}\) est donc une combinaison linéaire des vecteurs \(\overrightarrow{V}\) et \(\overrightarrow{W}\):
\(\overrightarrow{D} = \alpha \overrightarrow{V} + \beta \overrightarrow{W}\) avec \(\alpha = \overrightarrow{U} \cdot \overrightarrow{W}\) et \(\beta = - \overrightarrow{U} \cdot \overrightarrow{V}\)
Dans le cas de la base orthonormée directe \(\Big(\vec{i},\vec{j},\vec{k}\Big)\) nous avons :
\(\Big(\vec{i} \wedge \vec{j}\Big) \wedge \vec{k} = \Big(\vec{k} \wedge \vec{i}\Big) \wedge \vec{j} = \Big(\vec{j} \wedge \vec{k} \Big) \wedge \vec{i} = \vec{0}\)
\(\Big(\vec{i} \wedge \vec{j}\Big) \wedge \vec{i} = \vec{j}~ ;~ \Big(\vec{i} \wedge \vec{j}\Big) \wedge \vec{j} = -\vec{i} \quad \textrm{ etc}...\)
Propriétés de la multiplication scalaire
Non associativité : \(\overrightarrow{U} \wedge \Big(\overrightarrow{V} \wedge \overrightarrow{W} \Big) \ne \Big(\overrightarrow{U} \wedge \overrightarrow{V} \Big) \wedge \overrightarrow{W}\) (en général)
Le vecteur \(\overrightarrow{D} = \overrightarrow{U} \wedge \Big(\overrightarrow{V} \wedge \overrightarrow{W} \Big)\) se trouve dans le plan défini par \(\overrightarrow{V}\) et \(\overrightarrow{W}\)
alors que \(\overrightarrow{D'} = \Big(\overrightarrow{U} \wedge \overrightarrow{V} \Big) \wedge \overrightarrow{W}\) se situe dans le plan défini par \(\overrightarrow{U}\) et \(\overrightarrow{V}\).
Applications
Moment d'une force (résultante d'un produit vectoriel) par rapport à un point
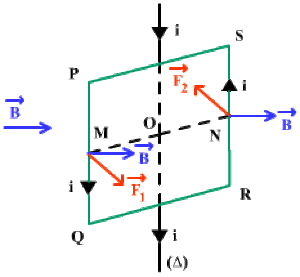
Un cadre rectangulaire mobile, autour de l'axe \((\Delta)\) placé dans un champ magnétique radial \(\overrightarrow{B}\), est parcouru par un courant d'intensité \(i\).
Les seules forces agissantes dans la rotation du cadre sont :\(\overrightarrow{F_{1}} =i ~\overrightarrow{PQ} \wedge \overrightarrow{B}\) et \(\overrightarrow{F_{2}} =i ~\overrightarrow{RS} \wedge \overrightarrow{B}\)
Les moments des forces \(\overrightarrow{F_{1}}\) et \(\overrightarrow{F_{2}}\) par rapport à \(O\) s'exprimeront à partir d'un double produit vectoriel :
\(\overrightarrow{m} ~\overrightarrow{F_{1}} /o = \overrightarrow{OM} \wedge \overrightarrow{F_{1}} = \overrightarrow{OM} \wedge \Big(i ~\overrightarrow{PQ} \wedge \overrightarrow{B} \Big)\)
\(\overrightarrow{m} ~\overrightarrow{F_{2}} /o = \overrightarrow{ON} \wedge \overrightarrow{F_{2}} = \overrightarrow{ON} \wedge \Big(i ~\overrightarrow{RS} \wedge \overrightarrow{B} \Big)\)
comme \(\overrightarrow{RS} = - \overrightarrow{PQ}\)
\(\overrightarrow{m} ~\Big(\overrightarrow{F_{1}} + \overrightarrow{F_{2}}\Big)/o =i ~\overrightarrow{NM} \wedge \Big(\overrightarrow{PQ} \wedge \overrightarrow{B} \Big)\)