Dérivées - Différentielles

La fonction \(f\) est définie pour \(x \in ] 0 ; + \infty [\) et pour :

\(\begin{array}{l l}x\in]0,1[&\color{blue}y=x^2\sqrt{-\ln x}\\x=1&\color{blue}y=0\\x>1&\color{blue}y=x^2\sqrt{\ln x}\end{array}\)

La courbe admet une branche parabolique de direction \(Oy.\)

La fonction est définie et continue sur \(] 0 ; + \infty [\)

\(\begin{array}{l l}Pour x\in]0,1[,&\color{blue}\ln x < 0 et \color{blue}y=x^2\sqrt{-\ln x}\\Pour x=1,&\color{blue}\ln x = 0 et \color{blue}y=0\\Pour x>1,&\color{blue}\ln x > 0 et \color{blue}y=x^2\sqrt{\ln x}\end{array}\)

Quand \(x \rightarrow +\infty\)

\(\lim_{x\rightarrow+\infty}\frac{y}{x}=\lim_{x\rightarrow+\infty}x\sqrt{\ln x}=+\infty\)

La courbe admet une branche parabolique de direction \(Oy.\)

Si \(x > 1,\) alors \(y'(x)=\frac{x}{2\sqrt{\ln x}}(4\ln x-1)\neq 0\) et \(y '(x)\) ne s'annule pas sur \(x \in ] 1 , + \infty[\)

Si \(x \in ] 0 , 1 [ ,\) alors \(y'(x)=\frac{x}{2\sqrt{-\ln x}}(-4\ln x-1)\) et \(y'(x)\) s'annule pour \(4 \ln x + 1 = 0,\) c'est à dire pour \(\boxed{x = e ^{-1/4}}\)

D'autre part :

\(\color{blue}\begin{array}{l l l} \lim_{x\rightarrow 0^+}y'(x)=0&\color{black}\textrm{et} &\lim_{x\rightarrow 1^-}y'(x)=-\infty\\&&\lim_{x\rightarrow 1^+}y'(x)=+\infty\end{array}\)

Calculons les dérivées suivantes :

Si \(x> 1\)

\(y = x^2\ln\sqrt{\ln x} \Rightarrow \color{blue} y'(x)=\frac{x}{2\sqrt{\ln x}}(4\ln x-1)\)

or \(4 \ln x + 1\) ne s'annule pas sur cet intervalle.

Si \(x \in ] 0 , 1[\)

\(y = x^2\ln\sqrt{-\ln x} \Rightarrow \color{blue} y'(x)=\frac{-x}{2\sqrt{-\ln x}}(4\ln x-1)\)

or \(4\ln x + 1 = 0\) pour \(x = e ^{-1/4}\in ] 0 , 1[\)

Tableau de variations de \(f\) :

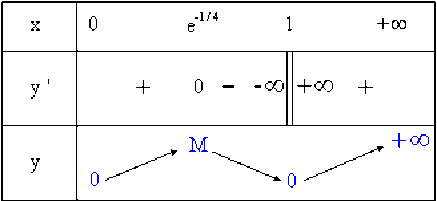
\(\color{blue}M\color{black} = (e^{-1/4})^2\sqrt{-\ln(e^{-1/4})}=\frac{1}{2}e^{-1/2}\approx\color{blue}0,3\)

En prolongeant la fonction par continuité au point zéro, nous pouvons calculer :

\(\lim_{x\rightarrow 0^+}\frac{y(x)-y(0)}{x-0}=\lim_{x\rightarrow 0^+}x\sqrt{|\ln x|} = 0\)

(Propriétés des croissances comparées)

La courbe à l'origine admet une demi tangente horizontale.

\(\textrm{quand }x\mapsto+1^-~~y'(x)=\frac{-x(4\ln x+1)}{2\sqrt{-\ln x}}~\textrm{et}~\color{blue}\lim_{x\rightarrow1^-}y'=-\infty\)

\(\textrm{quand }x\mapsto+1^+~~y'(x)=\frac{x(4\ln x+1)}{2\sqrt{\ln x}}~\textrm{et}~\color{blue}\lim_{x\rightarrow1^+}y'=+\infty\)

Le point de coordonnées \((1,0)\) est un point de rebroussement.

Pour \(x \in ] 0 , 1[\)

\(y''(x)=-\frac{8(\ln x)^2+6\ln x - 1}{4\ln x\sqrt{-\ln x}}\) et \(y''(x)=0\) pour \(\color{blue}x=e^{\frac{-3-\sqrt {17}}{8}}\)

Pour \(x > 1\)

\(y''(x)=\frac{8(\ln x)^2+6\ln x-1}{4\ln x\sqrt{\ln x}}\) et \(y''(x)=0\) pour \(\color{blue}x=e^{\frac{-3+\sqrt{17}}{8}}\)

Pour \(x \in ] 0, 1[ ,\) le calcul de \(y''(x)\) conduit à :

\(y''(x)=\frac{-2(4\ln x+5)\ln x+(4\ln x+1)}{4\ln x\sqrt{-\ln x}}=\color{blue}\frac{-8X^2-6X+1}{4X\sqrt{-X}}\)

avec \(\color{blue}X=\ln x\color{black}<0\)

d'où \(y''(x) = 0 \Rightarrow 8 X^2 + 6X - 1 = 0\) qui admet pour solutions : \(X=\frac{-3\pm\sqrt{17}}{8}\)

seule la valeur négative convient :

\(\boxed{X=\ln x=\frac{-3-\sqrt{17}}{8}\Rightarrow\color{blue}x=e^{\frac{-3-\sqrt{17}}{8}}}\)

Pour \(x > 1,\) nous avons :

\(y''(x)=\frac{2(4\ln x+5)\ln x-(4\ln x+1)}{4\ln x\sqrt{\ln x}}=\color{blue}\frac{8X^2+6X+1}{4X\sqrt{X}}\)

avec \(\color{blue}X=\ln x\color{black}>0\)

d'où \(y''(x) = 0 \Rightarrow 8 X^2 + 6X - 1 = 0\) qui admet pour solutions : \(X=\frac{-3\pm\sqrt{17}}{8}\)

seule la valeur positive convient :

\(\boxed{X=\ln x=\frac{-3+\sqrt{17}}{8}\Rightarrow\color{blue}x=e^{\frac{-3+\sqrt{17}}{8}}}\)