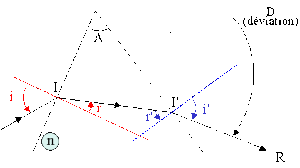
Le prisme
Partie
Les lois de Descartes relatives à la réfraction et les considérations géométriques dans le prisme, permettent d'écrire :
\(\sin i = n\sin r~~~~~\color{blue}(1)\\\color{black}\sin i' = n\sin r' ~~\color{blue}(2)\\\color{black}r+r'=A~~~~~~~~~~\color{blue}(3)\\\color{black}D=i+i'-A~~~~\color{blue}(4)\)
Ces quatre relations de sept variables, permettent d'exprimer la déviation \(D\) en fonction de trois variables indépendantes \(D = D (i, A, n).\) \((i\) : angle d'incidence du rayon d'incidence, \(A\) : angle du prisme, \(n\) : indice du verre).
Question
Déterminer, à \(A\) et \(n\) constants, la variation \((\frac{dD}{di})_{A, n}\)de la déviation \(D\) en fonction de \(i.\)
Aide simple
Procéder à la différenciation des quatre relations du prisme en tenant compte que \(A\) et \(n\) sont constants.
Aide détaillée
Différenciation de la relation \((1)\) du prisme :
\(\cos i~di = n\cos r ~dr\)
Appliquer cette méthode aux autres relations afin d'exprimer \(dD\) en fonction de \(di.\)
Aide méthodologique
Ne pas chercher à expliciter la fonction \(D = D (i, A, n)\) sous une forme classique.
Solution simple
Après avoir procédé à la différenciation des quatre relations, nous obtenons :
\(\boxed{(\frac{dD}{di})_{A,n}=1-\frac{\cos r'\cos i}{\cos r \cos i'}}\)
Solution détaillée
La différenciation des relations du prisme conduit à :
\(\color{blue}\begin{array}{c c}\cos i~di = n\cos r ~ dr&(1')\\\cos i'~di'=n\cos r'~dr'&(2')\\dr+dr'=0&(3')\\dD=di+di'&(4')\end{array}\)
En portant dans \((4'),\) l'expression de \(di'\) onbtenue dans \((2')\) :
\(dD=di+n\frac{\cos r'}{\cos i'}dr'\)
or d'après \((3')\) et \((1')\) :
\(dr'=-dr=-\frac{\cos i}{n\cos r}di\)
d'où
\(dD=di-\frac{n\cos r' \cos i}{n\cos r\cos i'}di\)
\(\boxed{(\frac{dD}{di})_{A,n}=1-\frac{\cos r'\cos i}{\cos r \cos i'}}\)
Question
Calculer l'angle d'incidence \(i_m,\) correspondant au minimum de déviation \(D_m\) d'un rayon incident après traversée du prisme.
Aide simple
La relation obtenue par\((\frac{dD}{di})_{A,n} = 0\) doit être exprimée en fonction des seules variables \(i\) et \(i'.\)
Aide détaillée
Elever au carré l'expression déduite de\((\frac{dD}{di})_{A,n} = 0\) et remplacer les \(\cos^2r\) et \(\cos^2r'\) en fonction de \(\sin^2i,\) \(\sin^2i'\) et \(n.\)
Aide méthodologique
Partir de la valeur de\((\frac{dD}{di})_{A,n}\) au minimum de déviation.
Solution simple
L'équation obtenue \(\sin^2i - \sin^2i' = 0\) a pour racine, physiquement accepatble :
\(i=i'=i_m\Rightarrow\color{blue}i_m=\frac{D_m+A}{2}\)
Solution détaillée
L'expression de conduit à
\(1-\frac{\cos r'\cos i}{\cos r\cos i'} = 0\Leftrightarrow\cos r\cos i'=\cos r'\cos i\)
En élevant au carré et en exprimant \(r\) et \(r'\) en fonction de \(i\) et \(i',\) on obtient :
\((1-\frac{\sin^2i}{n^2})(1-\sin^2i')=(1-\frac{\sin^2i'}{n^2})(1-\sin^2i)\)
qui se réduit à : \(\sin^2i - \sin^2i' = 0\) d'où \(i = \pm i'\)
La solution \(i = -i'\) est à écarter, car elle entraîne \(r = - r'\) et \(A = 0.\)
La racine acceptable est donc \(i = i' = i_m\) et d'après la relation \((4)\) du prisme :
\(D_m = i + i' - A = 2 i_m - A ,\) d'où
\(\boxed{\color{blue}i_m=\frac{D_m+A}{2}}\)
Question
En déduire l'indice \(n\) du prisme et son incertitude relative dans le cas d'une mesure \(\Delta\)
\(A = \Delta D_m.\) On effectuera le calcul de \(\Delta n/n\) par l'utilisation de la différentielle logarithmique.
Aide simple
Remplacer dans la relation \(\sin i = n \sin r,\) \(i\) et \(r\) par \(i_m\) et \(r_m.\)
Aide détaillée
Après avoir exprimé \(n\) comme quotient de deux sinus d'angles, prendre le logarithme \(\ln n\) puis sa différentielle logarithmique \(dn/n\) et enfin l'incertitude relative \(\Delta n/n.\)
Aide méthodologique
Utiliser une relation \((1)\) ou \((2)\) du prisme pour déterminer \(n.\)
Solution simple
Après substitution de \(i\) et \(r\) par \(i_m\) et \(r_m\) on obtient :
\(n=\frac{\sin\frac{A+D_m}{2}}{\sin\frac{A}{2}}\)
Le calcul de \(\Delta n/n\) conduit après simplification \(\Delta A = \Delta D_m\) à :
\(\boxed{\frac{\Delta n}{n} = \frac{1}{2}(\textrm{cotan} \frac{A}{2})\Delta A}\)
Solution détaillée
Au minimum de déviation, sachant que :
\(i=i'=i_m\Rightarrow\begin{cases}r=r'=r_m=A/2\\D_m=2i_m-A\Rightarrow i_m=\frac{A+D_m}{2}\end{cases}\)
La relation \((1)\) du prisme conduit à :
\(\sin i = n\sin r\\\sin i_m=n\sin r_m \Rightarrow \color{blue} n=\frac{\sin\frac{A+D_m}{2}}{\sin\frac{A}{2}}\)
Le calcul de \(\Delta n/n\) par l'utilisation de la différentielle logarithmique conduit à :
\(\ln n = \ln \sin\frac{A+D_m}{2}-\ln\sin\frac{A}{2}\)
\(\frac{dn}{n}=\frac{\cos\frac{A+D_m}{2}}{\sin\frac{A+D_m}{2}}d(\frac{A+D_m}{2})-\frac{\cos\frac{A}{2}}{\sin\frac{A}{2}}d(\frac{A}{2})\)
\(\frac{dn}{n} = \frac{1}{2}\textrm{cotan}\frac{A+D_m}{2}dD_m+\frac{1}{2}[\textrm{cotan}\frac{A+D_m}{2}-\textrm{cotan}\frac{A}{2}]dA\)
\(\frac{\Delta n}{n} = \frac{1}{2}|\textrm{cotan}\frac{A+D_m}{2}|\Delta D_m+\frac{1}{2}|\textrm{cotan}\frac{A+D_m}{2}-\textrm{cotan}\frac{A}{2}|\Delta A\)
Pour une incertitude absolue vérifiant \(\Delta A = \Delta D_m,\) nous avons :
\(\frac{\Delta n}{n} = \frac{1}{2}|\textrm{cotan}\frac{A+D_m}{2} - \textrm{cotan}\frac{A+D_m}{2} + \textrm{cotan}\frac{A}{2}|\Delta A\)
\(\boxed{\frac{\Delta n}{n}=\frac{1}{2}(\textrm{cotan}\frac{A}{2})\Delta A}\)