Antirésonance : circuit bouchon idéal
Partie
Question
Trois dipôles \(\displaystyle{D_1(R=4\textrm{ k}\Omega), D_2(L=25 \textrm{ mH}), D_3 (C = 20 \;\mu\textrm{F})}\) sont associés en parallèle et alimentés par un générateur délivrant une tension sinusoïdale de valeur efficace \(U = 100 \textrm{ V}.\)
Exprimer l'intensité dans chacune des branches de la dérivation en fonction de la fréquence.
En déduire l'intensité du courant débité par le générateur.
Calculer cette intensité pour une fréquence de \(50 \textrm{ Hz}\).
Pour quelle fréquence l'intensité du courant débité par le générateur est-elle minimale ? A cette fréquence, calculer l'intensité du courant dans chacun des dipôles.
Aide simple
La loi d'additivité des courants en régime permanent continu s'applique aussi aux valeurs instantanées des intensités, réelles et complexes.
Rappel de cours
Soit un dipôle dont la conductance varie avec la fréquence, alimenté par un générateur de courant délivrant une intensité constante. Si la conductance passe par un maximum, la tension aux bornes du dipôle sera alors maximale. A intensité constante à travers le dipôle, la tension passe par un maximum, ou, inversement, à tension constante aux bornes du dipôle, l'intensité passe par un minimum : ce phénomène est appelé antirésonance, et le circuit " bouchon " en est un exemple.
Circuit bouchon :
Ce circuit comprend trois dipôles en parallèle : un condensateur, une bobine, et un conducteur ohmique, supposés parfaits.
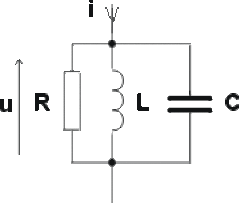
Les admittances complexes des trois branches ont pour expressions :
\(\displaystyle{\underline Y_1=\frac{1}{R};\;\underline Y_2=\frac{1}{jL\omega}}\)
\(\displaystyle{\underline Y_3=jC\omega}\)
L'admittance complexe de l'ensemble est donnée par leur somme :
\(\underline Y=\underline Y_1+\underline Y_2+\underline Y_3=\frac{1}{R}+\frac{1}{jL\omega}+jC\omega=\frac{1}{R}+j\Big(C\omega-\frac{1}{L\omega}\Big)=G+jH\)
La conductance \(G\) et la susceptance \(H\) ont donc pour expression :
\(\displaystyle{G=\frac{1}{R} ;\;H=C\omega-\frac{1}{L\omega}}\)
le déphasage de la tension \(u(t)\) aux bornes du circuit par rapport à l'intensité \(i(t)\) du courant est :
\(\displaystyle{\varphi=-\textrm{Arctg}\frac{H}{G}=\textrm{Arctg}\frac{1-LC\omega^2}{RC\omega}}\)
et l'admittance du dipôle s'écrit :
\(\displaystyle{Y=\sqrt{\frac{1}{R^2}+\Big(C\omega-\frac{1}{L\omega}\Big)^2}}\)
Ce circuit est appelé "anti-résonnant" ou "bouchon" parce que, quand la relation
\(\displaystyle{LC\omega^2 = 1}\) est vérifiée, son admittance \(Y\) est minimale, ce qui signifie que l'intensité du courant total dans le diviseur de courant est minimale. Le courant et la tension sont alors en phase. Une application est l'élimination, dans un signal composite, d'une fréquence particulière. Dans le montage pratique, \(R\) représente alors la résistance de fuite du condensateur, qui est en général très grande, ce qui conduit à une faible valeur de \(Y\).
Aide méthodologique
Orientation : Loi d'Ohm en régime sinusoïdal permanent
Solution simple
\(\displaystyle{i_1=\frac{U}{R}\sqrt{2}\cos\omega t;\;i_2=\frac{U}{L\omega}\sqrt{2}\cos(\omega t-\frac{\pi}{2});\;i_3=C\omega U\sqrt{2}\cos(\omega t+\frac{\pi}{2})}\)
\(\displaystyle{i(t)=i_1+i_2+i_3=U\sqrt{2}\Big(\frac{1}{R^2}+(C\omega-\frac{1}{L\omega})^2\Big)^{1/2}\cos(\omega t+\varphi)}\)
\(\displaystyle{\varphi=\textrm{Arctg}\Big(\frac{LC\omega^2-1}{RL\omega}\Big)}\)
\(\displaystyle{I = 12,10 \textrm{ A}}\)
\(\displaystyle{F_0 = 225 \textrm{ Hz} ; I_1 = I_{\textrm{min}} = 25 \textrm{ mA} ; I_2 = I_3 = 2,83 \textrm{ A}}\)
Solution détaillée
1) Le montage étudié correspond au schéma ci-contre :
Les admittances complexes des trois branches ont pour expressions :
\(\displaystyle{\underline Y_1=\frac{1}{R}\quad\underline Y_2=\frac{1}{jL\omega}\quad\underline Y_3 = jC\omega}\)
soit u(t) la tension appliquée au bornes du dipôle : c'est la même aux bornes de chacune des trois branches, et l'on peut écrire, pour chacune : \(\displaystyle{\underline i(t)=\underline Y.\underline u(t)}\) , en utilisant les écritures complexes des intensités et des tensions.
D'où, avec \(\displaystyle{\underline u(t)=U\sqrt{2}.\textrm{e}^{j\omega t}}\) :
\(\displaystyle{\underline i_1(t)=\frac{U}{r}\sqrt{2}.\textrm{e}^{j\omega t};\;\underline i_1(t)=\frac{U}{r}\sqrt{2}.\cos\omega t}\)
\(\displaystyle{\underline i_2(t)=\frac{1}{jL\omega}U\sqrt{2}.\textrm{e}^{j\omega t};\;\underline i_2(t)=\frac{1}{jL\omega}U\sqrt{2}.\cos(\omega t-\pi/2)}\)
\(\displaystyle{\underline i_3(t)=jC\omega.U\sqrt{2}.\textrm{e}^{j\omega t};\;\underline i_3(t)=C\omega.U\sqrt{2}.\cos(\omega t+\pi/2)}\)
2) La loi d'additivité des courants en régime permanent continu s'applique aussi aux valeurs instantanées des intensités complexes :
\(\displaystyle{\underline i(t)=\underline i_1(t)+\underline i_2(t)+\underline i_3(t)}\)
\(\displaystyle{\begin{array}{lll}\underline i(t)&=&U\sqrt{2}.\textrm{e}^{j\omega t}\Bigg(\frac{1}{R}+j\Bigg(C\omega-\frac{1}{L\omega}\Bigg)\Bigg)\\ & = & I\sqrt{2}.\textrm{e}^{j(\omega t+\varphi)}\end{array}}\)
d'où l'intensité efficace : \(\displaystyle{I=U\Big(\frac{1}{R^2}+(C\omega-\frac{1}{L\omega})^2\Big)^{1/2}}\)
et le déphasage : \(\displaystyle{\varphi=\textrm{Arctg}\Big(\frac{LC\omega^2-1}{RL\omega}\Big)}\)
3) pour \(F = 50 \textrm{ Hz}\), les intensités efficaces dans les trois branches sont :
\(\displaystyle{I_1=\frac{U}{R}=\frac{100}{4.10^3}=25\textrm{ mA}}\)
\(\displaystyle{I_2=\frac{U}{L\omega}=\frac{100}{25.10^{-3}.100\pi}=12.73\textrm{ A}}\)
\(\displaystyle{I_3=U.C\omega=100.20.10^{-6}.100\pi=0,628\textrm{ A}}\)
et l'intensité dans le circuit principal :
\(\displaystyle{I=U\left(\frac{1}{R^2}+\Big(C\omega-\frac{1}{L\omega}\Big)^2\right)^{1/2}} = 100\Bigg(\frac{1}{(4.10^{3})^{2}} + \Big(20. 10^{-6}. 100 \pi - \frac{1}{25.10^{-3}.100\pi}\Big)^{2}\Bigg)^{1/2} = \mathrm{12,10~A}\)
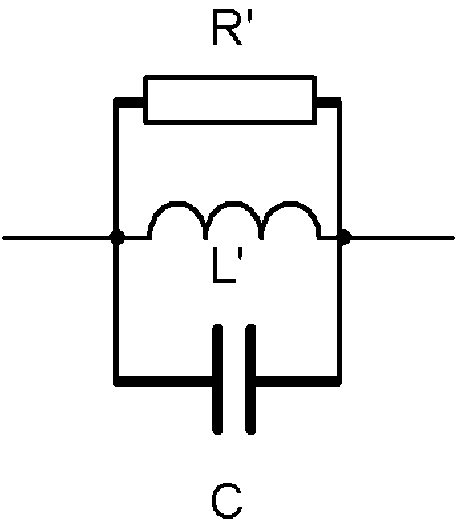
4) Le montage étudié correspond au schéma ci-contre :
Les admittances complexes des trois branches ont pour expressions :
\(\displaystyle{\underline Y_1=\frac{1}{R}}\)
\(\displaystyle{\underline Y_2=\frac{1}{jL\omega}}\)
\(\displaystyle{\underline Y_3=jC\omega}\)
L'admittance complexe de l'ensemble est donnée par leur somme :
\(\displaystyle{\underline Y=\underline Y_1+\underline Y_2+\underline Y_3=\frac{1}{R}+\frac{1}{jL\omega}+jC\omega=\frac{1}{R}+j\Big(C\omega-\frac{1}{L\omega}\Big)}\)
le déphasage de la tension \(u(t)\) aux bornes du circuit par rapport à l'intensité \(i(t)\) du courant est : \(\displaystyle{\varphi=\textrm{ Arctg}\frac{1-LC\omega^2}{RC\omega}}\)
et l'admittance du dipôle s'écrit : \(\displaystyle{Y=\sqrt{\frac{1}{R^2}+\Big(C\omega-\frac{1}{L\omega}\Big)^2}}\)
Quand la relation \(\displaystyle{LC\omega^2=1}\) est vérifiée, l'admittance\(Y\) est minimale, ce qui signifie que l'intensité du courant total dans le diviseur de courant est minimale et vaut \(\displaystyle{I_{\textrm{min}} = Y_{\textrm{min}}.U = U/R}\).
Le courant et la tension sont alors en phase. D'où la fréquence d'antirésonance : \(\displaystyle{F_0=\frac{1}{2\pi\sqrt{LC}}}\)
Application numérique : \(\displaystyle{F_0=225\textrm{ Hz}}\)

Et les intensités à cette fréquence :
\(\displaystyle{I_1=\frac{U}{R}=I_{\textrm{min}}=25\textrm{ mA}}\)
\(\displaystyle{I_2=\frac{U}{L\omega_0}=2,83\textrm{ A}}\)
\(\displaystyle{I_3=U.C\omega_0=2,83\textrm{ A}}\)
Remarque : les courants \(I_2\) et \(I_3\) ont même valeur, mais sont déphasés de \(\pi\) ; leur somme est donc nulle.