Dipôle équivalent à deux condensateurs
Partie
Question
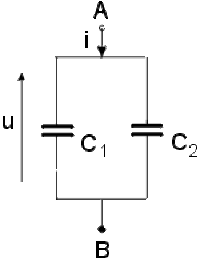
Déterminer l'admittance équivalente au dipôle ci-dessous, vu de \(A\) et \(B.\)
En déduire son impédance.
Aide simple
\(\displaystyle{\underline Y=\sum_n\underline Y_n}\)
Aide détaillée
\(\displaystyle{\underline Y = jC\omega}\)
Aide méthodologique
Loi d'Ohm en régime sinusoïdal
Solution simple
\(\displaystyle{\underline Y_{AB} = j(C_1 + C_2) \omega; \underline Z_{AB} = \frac{1}{j(C_1 + C_2)\omega}}\)
Solution détaillée
L'admittance complexe du dipôle équivalent à une association de dipôles en parallèle est égale à la somme des admittances complexes : \(\displaystyle{\underline Y=\sum_n\underline Y_n}\)
Pour un condensateur de capacité \(C\), l'admittance complexe est \(\displaystyle{\underline Y_c = jC\omega}.\)
D'où : \(\displaystyle{\underline Y_{AB} = y(C_1) + y(C_2) = jC_1 \omega + jC_2 \omega = j(C_1 + C_2)\omega}\)
et \(\displaystyle{\underline Z_{AB}=\frac{1}{\underline Y_{AB}}=\frac{1}{j(C_1+C_2)\omega}}\)