Approche analytique
Mathématiquement, l'équation précédente \(q"(t)~+~\omega^2_0~q(t) = 0\) est une équation différentielle linéaire du second ordre à coefficients constants, de forme générale :
\(ay" + by' + cy = 0\)
En identifiant terme à terme les deux types d'équations mathématique et physique, il vient :
\(a = 1\), \(b = 0\), \(c = \omega^2_0\) et \(y(x) \Leftrightarrow q(t)\).
L'expression de la solution générale \(q(t)\) se déduit de la résolution de l'équation \(ay" + by' + cy = 0\), que l'on suppose connue. On rappelle que le discriminant de l'équation caractéristique associé à l'équation différentielle s'écrit \(\Delta = b^2 - 4 ~a~c\).
On pose habituellement \(\alpha = - \frac{b}{2a}\) et \(\beta = \frac{\sqrt{4 ~a~c - b^2}}{2~a}\), soit ici \(\Delta = - 4 \omega^2_0\). On constate que \(\Delta\) est toujours négatif.
Cette résolution montre que \(q(t)\) s'écrit sous l'une des trois formes équivalentes suivantes :
\(q(t) = C ~\cos ~\omega_0t + D ~\sin ~\omega_0 t\) \(\qquad\) \(q(t) = q_m~ \cos (\omega_0 t ~+ \varphi)\) \(\qquad\) \(q(t) = q_m~ \sin (\omega_0 t ~+ \Psi)\)
On constate que \(q(t)\) dépend de deux constantes \((C,D)\), \((q_m, \varphi)\) ou \((q_m, \Psi)\). Il faut se donner deux relations pour les déterminer. La réponse \(q(t)\) est alors unique.
Dans un problème physique, ces deux relations décrivent l'état initial du système, elles sont appelées conditions initiales ; elles s'écrivent, à \(t = 0\) :
\(q(t = 0) = q_0~~\) et \(~~q'(t = 0) = q'_0\)
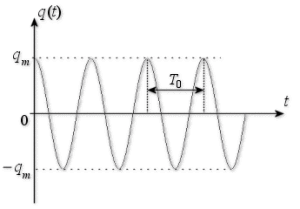
La réponse \(q(t)\) est harmonique. On retrouve la définition de l'oscillateur harmonique donné dans l'introduction.
\(q_m\) et \(\varphi\) représentent respectivement l'amplitude et la phase initiale de la loi \(q(t)\) de période propre \(T_0 = \frac{2\pi}{\omega_0}\). Au point de vue des unités, \(q_m\) s'exprime avec la même unité que \(q\) ; \(\varphi\) et \(T\) s'expriment respectivement en radian et en seconde.
Réponse d'un oscillateur harmonique de pulsation propre w0
Les conditions initiales choisies sont : \(q(t = 0) = q_0 > 0\) et \(q' (t = 0) = 0\). On montre dans ce cas que \(q_m = q_0\) et \(\varphi = 0\) et par suite \(q(t)\) s'écrit \(q(t) = q_0~\cos\omega_0 t\)
Relation entre les constantes
En développant \(\cos (\omega_0 t + \varphi)\) et en identifiant terme à terme les deux premières solutions de \(q(t)\) on obtient les relations : \(C = q_m~\cos \varphi\) et \(D = -q_m~\sin \varphi\).
On en déduit : \(q_m = \sqrt{C^2 + D^2}\) et \(\tan \varphi = \frac{-D}{C}\).
Autre relation : \(\Psi = \varphi + \pi / 2\).
Propriété de l'oscillateur harmonique
La période \(T_0\) est indépendante de l'amplitude des oscillations. Il y a isochronisme des oscillations.
Remarque : Résolution de l'équation différentielle
Rappelons que l'on montre en mathématique que la solution générale d'une équation différentielle telle que \(q" + \omega^2_0~ q = 0\) (ou \(ay" + by' + cy = 0\) dans le cas général), est égale à une combinaison linéaire de deux solutions linéairement indépendantes \(q_1(t)\) et \(q_2(t)\). Dans le cas considéré, on vérifie facilement que les fonctions \(q_1\) et \(q_2\) définies par \(q_1(t) = \cos~\omega_0 ~t\) et \(q_2(t) = \sin~\omega_0 ~t\), satisfont à ces conditions. La solution générale s'écrit donc \(q(t) = C \cos~\omega_0~t + D \sin~\omega_0~t\)
On retrouve de façon simple l'expression de \(q(t)\) donnée précédemment.