Oscillateur électrique : circuit série (R, L, C)
Considérons le circuit série (R, L, C) alimenté par un générateur de tension de f.é.m. \(u(t) = U_m \cos \Omega t\), \(u(t)\) représente l'excitation appliquée au circuit série.
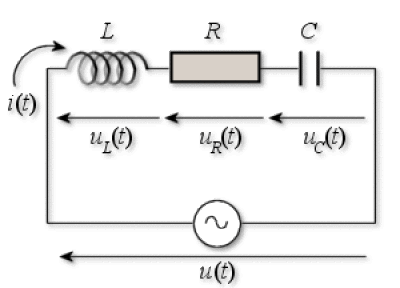
A partir de l'écriture de la loi d'ohm :
\(u_L + u_R + u_C = u~~~~\), \(~~~~L\frac{di}{dt} + Ri + \frac{1}{C}\int i \mathrm dt = U_m \cos \Omega t\)
Nous obtenons :
en dérivant par rapport à \(t\) et en divisant par \(L\), l'équation en intensité :
\(i"(t) + \frac{R}{L}~i'(t) + \frac{1}{LC}~i(t) = -\frac{\Omega ~U_m}{L} \sin ~\Omega~t = \frac{\Omega~ U_m}{L} \cos\Big(\Omega~ t + \frac{\pi}{2}\Big)\)
l'équation par rapport à la charge instantanée \(q(t)\) du condensateur, en rappelant que
\(i(t) = q'(t)\) :
\(q"(t) + \frac{R}{L}q'(t) + \frac{1}{LC}q(t) = \frac{U_m}{L} \cos \Omega t\)
l'équation par rapport à la d.d.p. aux bornes du condensateur \(u_C(t)\), en rappelant que
\(u_C(t) = \frac{q(t)}{C}\) :
\(u''_C(t) + \frac{R}{L}~ u'_C(t) + \frac{1}{L C} ~u_C(t) = \frac{U_m}{LC} \cos ~\Omega t\)
Sachant que \(\frac{R}{2 L} = \lambda\) et \(\frac{1}{LC} = \omega_0^2\), les trois équations différentielles ci-dessus sont du type oscillateur harmonique forcé et amorti, de coefficient d'amortissement \(\lambda = \frac{R}{2 L}\) et de pulsation propre \(\omega_0 = \sqrt{\frac{1}{LC}}\)
On remarque que le second membre de chacune des équations ci-dessus, \(h(t)\), est différent de l'excitation \(u(t)\).