Réponse à un échelon de tension
Partie
On réalise un circuit comportant un générateur muni d'un interrupteur, débitant dans une bobine \(v_\mathrm A-v_\mathrm B=\mathrm E\) montée en parallèle avec une résistance \(\mathrm R\). La résistance interne du générateur est négligeable.
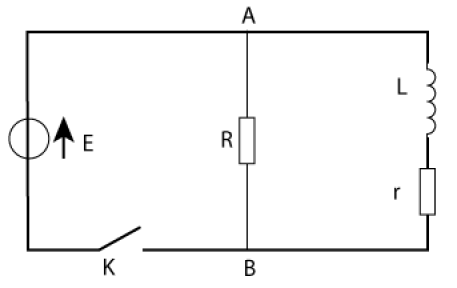
Question
A l'instant \(t=0\), on ferme l'interrupteur. Etablir les équations des intensités des courants dans la bobine et dans la résistance.
Aide simple
La tension est la même aux bornes des 3 branches
Aide détaillée
Le générateur de tension est idéal : \(v_\mathrm A-v_\mathrm B=\mathrm E\) quel que soit le courant débité
Solution simple
\(i_\mathrm R=\mathrm{E/R}\); \(i_\mathrm L=(\mathrm{E/r})(1-\mathrm e^{-t/\tau})\)
Solution détaillée
Une fois l’interrupteur \(\mathrm K\) fermé, la tension est la même aux bornes des 3 branches :
\(\displaystyle{v_\mathrm B-v_\mathrm A=\mathrm E=\mathrm R.i_R(t)=\mathrm r.i_L(t)+\mathrm L\frac{\mathrm di_L}{\mathrm dt}}\)
d'où : \(\displaystyle{i_R(t)=\frac{\mathrm E}{\mathrm R}=\mathrm{cste}}\)
et : \(\displaystyle{\mathrm r.i_L(t)+\mathrm L\frac{\mathrm di_L}{\mathrm dt}=\mathrm E}\)
en divisant par r : \(\displaystyle{i_L(t)+\frac{\mathrm L}{\mathrm r}\frac{\mathrm di_L}{\mathrm dt}=\mathrm E\Leftrightarrow i_L(t)+\tau\frac{\mathrm di_L}{\mathrm dt}=\frac{\mathrm E}{\mathrm r}}\)
avec \(\displaystyle{\tau=\frac{\mathrm L}{\mathrm r}}\)
la solution de cette équation différentielle est de la forme :\(i_L(t)=\mathrm{A.e}^{-t/\tau}+SP\), où \(SP\) est une solution particulière de l’équation complète. Comme le second membre est constant, on cherche une solution particulière \(i_L\) constante. En faisant \(\displaystyle{\frac{\mathrm di_L}{\mathrm dt}=0}\) dans l’équation complète, il vient : \(\displaystyle{i_L=\frac{\mathrm E}{\mathrm r}}\), d’où la solution générale : \(\displaystyle{i_L(t)=\mathrm{A.e}^{-t/\tau}+\frac{\mathrm E}{\mathrm r}}\). L'intensité dans la bobine varie de façon continue. Comme jusqu'à la fermeture de l'interrupteur, aucun courant ne circule dans le circuit : \(\displaystyle{i_L(0)=\mathrm A+\frac{\mathrm E}{\mathrm r}=0}\). D'où :\(\displaystyle{\mathrm A=-\frac{\mathrm E}{\mathrm r}}\) et \(\displaystyle{i_L(t)=\frac{\mathrm E}{\mathrm r}\left(1-\mathrm e^{-t/\tau}\right)}\)dont la valeur limite, pour \(t\) tendant vers l'infini, est \(\displaystyle{\frac{\mathrm E}{\mathrm r}}\).
Question
Une fois le régime permanent établi, on ouvre l'interrupteur. Etablir la nouvelle équation du courant circulant dans la bobine. En déduire la différence de potentiel \(v_\mathrm A-v_\mathrm B\). Montrer qu'à l'instant de l'ouverture, elle peut être supérieure à \(\mathrm E\).
Aide simple
La tension est la même aux bornes des 3 branches
Aide détaillée
Le générateur de tension est idéal : \(v_\mathrm A-v_\mathrm B=\mathrm E\) quel que soit le courant débité
Solution simple
\(i(t)=(\mathrm{E/r) }\mathrm e^{-t/\tau}\); à \(t=0\), \(v_\mathrm B-v_\mathrm A=\mathrm{R.E/r}>\mathrm E\) si \(\mathrm r>\mathrm R\)
Solution détaillée
Quand l’interrupteur est réouvert, il n’y a plus qu’une maille, dans laquelle circule un courant d’intensité \(i(t)\).
D’après la loi des mailles :
\(\displaystyle{\mathrm R.i(t)+\mathrm r.i(t)+\mathrm L\frac{\mathrm di}{\mathrm dt}=0\Leftrightarrow (\mathrm R+\mathrm r).i(t)+\mathrm L\frac{\mathrm di}{\mathrm dt}=0\Leftrightarrow i(t)+\tau'.\mathrm L\frac{\mathrm di}{\mathrm dt}=0}\), avec \(\displaystyle{\tau'=\frac{\mathrm L}{\mathrm r+\mathrm R}}\).
Comme le second membre est nul, la solution de cette équation différentielle est : \(i(t')=\mathrm{A.e}^{-t'/\tau}\), avec \(t’ = 0\) quand l’interrupteur est rouvert. A cette date, le régime permanent précédent est atteint et le courant dans la bobine a atteint sa valeur limite \(\displaystyle{\frac{\mathrm E}{\mathrm r}}\). Comme l’intensité dans la bobine varie de façon continue, \(\displaystyle{i(0)=\mathrm A=\frac{\mathrm E}{\mathrm r}}\). Aux bornes de \(\mathrm R\), pour \(t'=0\), la différence de potentiel est donc :
\(\displaystyle{(v_\mathrm B-v_\mathrm A)_{t'=0}=\mathrm R.i(0)=\mathrm E\frac{\mathrm R}{\mathrm r}>\mathrm E}\)