Réponse à un échelon de courant
Partie
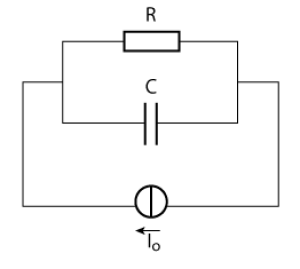
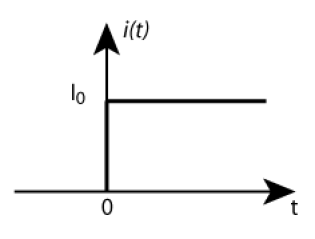
La figure ci-contre représente un générateur de courant idéal, pour lequel l'intensité qu'il débite est indépendante du circuit relié à ses bornes. A l'instant \(t=0\), on met en marche ce générateur, créant un échelon de courant \(i(t)\).
Question
Le générateur débite dans le circuit \(\mathrm{RC}\) parallèle ci-contre. On note \(i_C\) l'intensité du courant dans la branche où se trouve le condensateur, \(i_R\) l'intensité du courant dans l'autre branche.
Quelle relation lie les trois intensités?
Quelle est la relation entre la charge \(q\) du condensateur, \(\mathrm C\), \(\mathrm R\) et \(i_R\)?
Quelle est la relation entre la charge \(q\) du condensateur et \(i_C\)?
Ecrire ces relations pour \(t<0\), puis pour \(t\ge0\). En déduire la valeur de \(q\) pour \(t=0\).
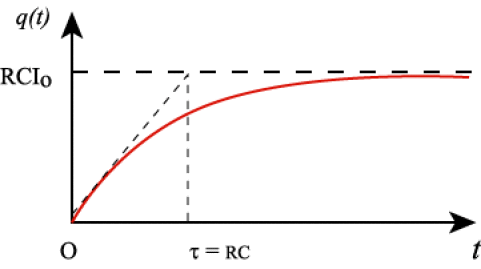
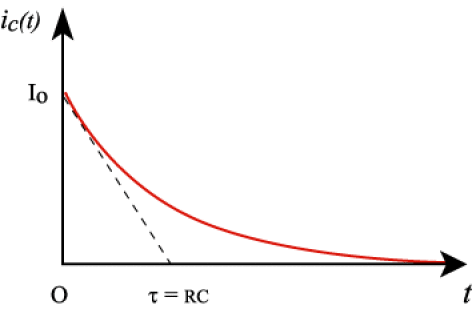
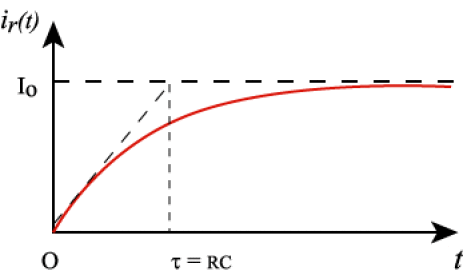
Donner les équations de \(q(t)\),\(i_C(t)\), \(i_R(t)\) et tracer les graphes correspondants.
Aide simple
Le générateur de courant est idéal : \(i_\mathrm C(t)+i_\mathrm R(t)=I_0\forall t\);
La tension est la même aux bornes des deux dipôles.
Aide détaillée
L'intensité dans la branche où est \(\mathrm C\) est due à la variation de charge du condensateur :
\(i(t)=\mathrm dq/\mathrm dt\).
Solution simple
\(i_\mathrm C(t)+i_\mathrm R(t)=I_0\); \(\mathrm R.i_\mathrm R(t)=q(t)/\mathrm C\);
\(t<0\): \(i_\mathrm C(t)=i_\mathrm R(t)=0\), \(q(0)=0\);
\(t>0\): \(q(t)+\mathrm{RC}(\mathrm dq/\mathrm dt)=\mathrm{RC}I_0\); \(q(t)=\mathrm{RC}I_0(1-\mathrm e^{-t/\tau})\),
avec \(\tau=\mathrm{RC}\) ; \(i_C(t)=I_0\mathrm e^{-t/\tau}\);\(i_\mathrm R(t)=I_0(1-\mathrm e^{-t/\tau})\)
Solution détaillée
Circuit \(\mathrm{RC}\) parallèle :
L'intensité \(i(t)\) se répartit entre les deux branches ; d'après la loi aux nœuds : \(i_\mathrm C+i_\mathrm R=i(t)\)
- La tension est la même aux bornes des deux dipôles :
\(\displaystyle{\mathrm R.i_\mathrm R=\frac{\mathrm q}{\mathrm C}}\)
d'où : \(\displaystyle{i_\mathrm R=\frac{\mathrm q}{\mathrm R.\mathrm C}}\)
- dans la branche où se trouve le condensateur l'intensité du courant est liée aux variations de la charge par : \(\displaystyle{i_\mathrm C=\frac{\mathrm dq}{\mathrm dt}}\)
en remplaçant \(i_\mathrm C\) et \(i_\mathrm R\) par leurs expressions :
\(\displaystyle{\frac{\mathrm dq}{\mathrm dt}+\frac{\mathrm q}{\mathrm R.\mathrm C}=i(t)}\)
en multipliant par \(\mathrm{RC}\) :
\(\displaystyle{\mathrm{RC}\frac{\mathrm dq}{\mathrm dt}+\mathrm q=\mathrm{RC}i(t)}\)
pour \(t<0\), \(i(t)=0=\mathrm{cste}\) d'où la solution particulière \(\mathrm q=\mathrm{cste}=0\) pour \(t\ge0\), \(i(t)=I_0\), d'où :
Cette équation différentielle admet pour solution :
\(q(t)=\mathrm{A.e}^{-t/\tau}+\mathrm{cste}\)
puisque le second membre \(\mathrm{RCI}_0\) est constant ; en faisant \(\mathrm dq/\mathrm dt=0\), il vient :
\(\mathrm q=\mathrm{RCI}_0\)
d'où la solution complète
\(q(t)=\mathrm{RCI}_0+\mathrm{A.e}^{-t/\tau}\)
comme pour \(t\le0\), \(q(t)=0\)
\(\mathrm A=-\mathrm{RCI}_0\)
et finalement :
\(q(t)=\mathrm{RCI}_0(1-\mathrm e^{-t/\tau})\)
comme \(\displaystyle{i_\mathrm C=\frac{\mathrm dq}{\mathrm dt}}\), \(i_\mathrm C=\mathrm I_0\mathrm{ e}^{-t/\tau}\)
\(\displaystyle{i_\mathrm R=\frac{\mathrm q}{\mathrm{RC}}=\mathrm I_0\left(1-\mathrm e^{-t/\tau}\right)^t}=\mathrm I_0-i_\mathrm C\)
Question
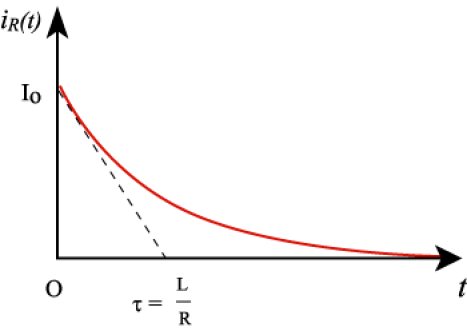
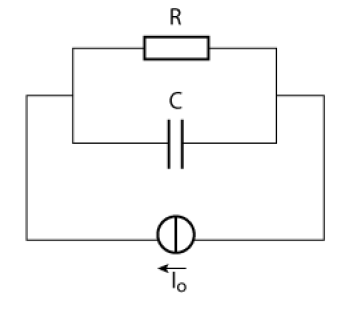
Le générateur débite dans un circuit \(\mathrm{RL}\) parallèle. On note \(i_\mathrm L\) l'intensité du courant dans la branche où se trouve la bobine, \(i_\mathrm R\) l'intensité du courant dans l'autre branche. La bobine est supposée idéale, c'est à dire que sa résistance est négligeable.
Quelle relation lie les trois intensités?
Etablir l'équation différentielle donnant \(i_\mathrm L(t)\). Résoudre cette équation. En déduire \(i_\mathrm R(t)\) et tracer les deux graphes correspondants.
Aide simple
Le générateur de courant est idéal : \(i_\mathrm L(t)+i_\mathrm R(t)=I_0\forall t\)
La tension est la même aux bornes des deux dipôles.
Aide détaillée
Au bornes de \(\mathrm L\): \(\displaystyle{u(t)=\mathrm L.\frac{\mathrm di}{\mathrm dt}}\)
Solution simple
\(i_\mathrm L(t)+i_\mathrm R(t)=I_0\); \(i_\mathrm L(t)+\tau(\mathrm di_\mathrm L/\mathrm dt)=I_0\),
avec \(i_\mathrm L(t)+i_\mathrm R(t)=I_0\); \(i_\mathrm L(t)+\tau(\mathrm di_\mathrm L/\mathrm dt)=I_0\),
Solution détaillée
Circuit \(\mathrm{RL}\) parallèle
- d'après la loi des nœuds :
\(i_\mathrm R+i_\mathrm L=i(t)\)
- la tension aux bornes des deux dipôles est la même :
\(\displaystyle{\mathrm R.i_\mathrm R=-\mathrm L\frac{\mathrm di_\mathrm L}{\mathrm dt}}\)
comme : \(i_\mathrm R=i(t)-i_\mathrm L\)
\(\displaystyle{\mathrm R(i(t)-i_\mathrm L)=-\mathrm L\frac{\mathrm di_\mathrm L}{\mathrm dt}}\)
\(\displaystyle{\mathrm R.i_\mathrm L+\mathrm L\frac{\mathrm di_\mathrm L}{\mathrm dt}=\mathrm Ri(t)}\)
en divisant par R :
\(\displaystyle{i_\mathrm L+\frac{\mathrm L}{\mathrm R}\frac{\mathrm di_\mathrm L}{\mathrm dt}=i(t)}\)
équation différentielle dont la solution est :
\(i_\mathrm L(t)=\mathrm{Ae}^{-t/\tau}+\mathrm{cste}\)
puisque le second membre est une constante ; pour \(t\ge0\), \(i(t)=\mathrm I_0\); en faisant \(\frac{di_{L}}{dt}=0\), il vient la solution particulière : \(i=\mathrm I_0\)
d'où la solution générale :
\(i_\mathrm L(t)=\mathrm{Ae}^{-t/\tau}+\mathrm I_0\)
pour \(t\le0\), \(i(t)=0\) donc \(i_\mathrm R=i_\mathrm L=0\) d'où \(\mathrm A=-\mathrm I_0\); finalement :
\(i_\mathrm L(t)=\mathrm I_0(1-\mathrm e^{-t/\tau})\)
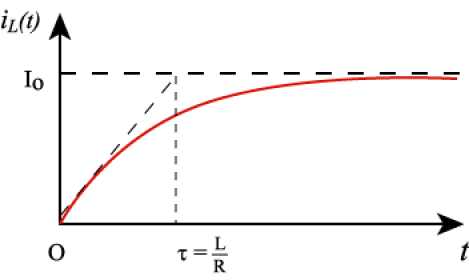
et \(\displaystyle{i_\mathrm R=-\frac{\mathrm L}{\mathrm R}\frac{\mathrm di_\mathrm L}{\mathrm dt}=\mathrm I_0-i_\mathrm L=\mathrm I_0\mathrm e^{-t/\tau}}\)