Résultat général
On n'a considéré jusqu'à présent que la propagation d'une onde électromagnétique dans un milieu homogène et isotrope, en dehors des charges et des courants.
On s'intéresse maintenant aux conditions de passage d'une onde électromagnétique à travers la surface de séparation entre deux milieux (notés par les indices 1 et 2) supposés eux-mêmes homogènes et isotropes.
Cependant, les deux milieux étant différents, il y a donc une discontinuité au niveau du dioptre constitué par la surface de séparation, ce qui interdit que l'on puisse utiliser les équations de Maxwell caractéristiques des milieux homogènes et isotropes : dans ces conditions, \(\vec B\) n'est pas proportionnel à \(\vec H\), et \(\vec D\) n'est pas proportionnel à \(\vec E\).
Le comportement de l'onde électromagnétique sera donc obtenu à partir des quatre équations de Maxwell (revoir le tableau de synthèse, § A.2.a, qui fait intervenir \(\vec E\), \(\vec B\), \(\vec D\) et \(\vec H\)).
Si l'on se place en dehors de la présence de charges (\(\rho = 0\)) et de courants (\(\vec j = 0\)), de sorte que ces équations s'écrivent :
\(\overrightarrow{\mathrm{rot}} ~ \vec E = - \frac{\partial \vec B}{\partial t} ~, \qquad \overrightarrow{\mathrm{rot}} ~ \vec H = \frac{\partial \vec D}{\partial t} ~, \qquad \mathrm{div} ~ \vec D = 0 ~, \qquad \mathrm{div} ~ \vec B = 0\)
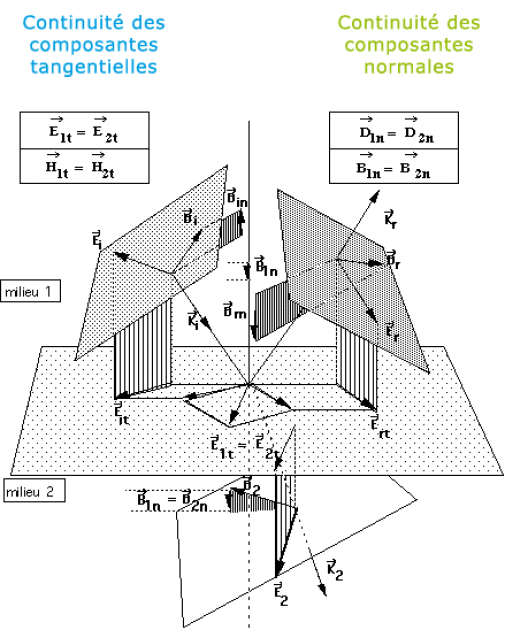
En appliquant ces équations (et les théorèmes généraux rappelés au § A.2.a), on démontre 2 types de relations, valables au voisinage immédiat du dioptre et concernant la continuité des composantes tangentielles au dioptre [pour les champs \(\vec E\) et \(\vec H\)] et la continuité des composantes normales au dioptre [pour les champs \(\vec B\) et \(\vec D\)].
La démonstration de ces résultats est reportée en annexe (§ A.5 - "Annexe : démonstration").
Par contre, sur un dioptre métallique où il existera en général une densité de courant de surface \(( \vec j \ne \vec 0 )\), la démonstration des relations de continuité devra utiliser les relations de Maxwell :
\(\overrightarrow{\mathrm{rot}} ~ \vec E = - \frac{\partial \vec B}{\partial t}~,\qquad \overrightarrow{\mathrm{rot}} ~ \vec H = \vec j + \frac{\partial \vec D}{\partial t}~, \qquad \mathrm{div} ~ \vec D = \rho ~, \qquad \mathrm{div} ~ \vec B = 0\)
avec éventuellement \(\rho = 0\)
... en présence de charge et de courants de surface :
\(\vec E_{2t} = \vec E_{1t}\)
\(\vec H_{2t} = \vec H_{1t} + \vec j_s \wedge \vec n\)
\(\vec D_{1n} = \vec D_{2n} + \sigma\)
\(\vec B_{1n} = \vec B_{2n}\)
où \(\vec j_s\) est la densité de courant sur la surface du dioptre et \(\sigma\) la densité de charges sur la surface du dioptre.
... en dehors des charges et des courants :
Le schéma ci-dessus représente les champs au voisinage immédiat du dioptre de part et d'autre de sa surface.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
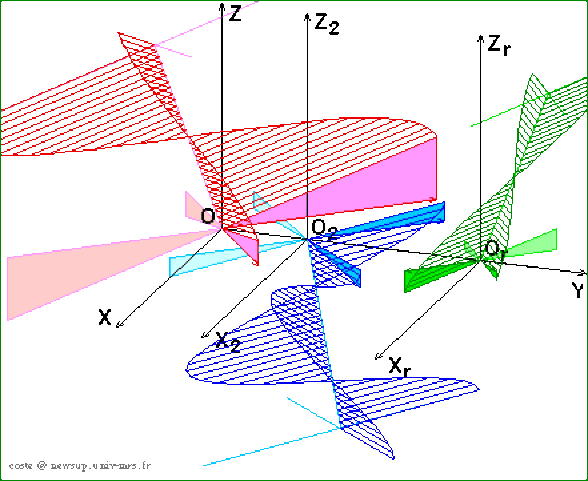
La simulation ci-dessus représente la propagation des champs incident, réfléchi et transmis.
Les 3 points \(O\), \(O_2\) et \(O_r\) devraient être confondus.
Ils ont été écartés pour une meilleure clarté du schéma.
Le schéma et la simulation ci-dessus représentent le voisinage immédiat du dioptre de part et d'autre de sa surface.
Propriété :
Le résultat suivant est supposé admis :
Si l'onde incidente \(( \vec E_i, \vec B_i )\) est plane dans le milieu (1), alors :
l'onde réfléchie \(( \vec E_r, \vec B_r )\) dans le milieu (1)
et l'onde transmise \(( \vec E_2, \vec B_2 )\) dans le milieu (2)
sont également planes.
En particulier : les trièdres \(( \vec E_i, \vec B_i, \vec K_i )\), \(( \vec E_r, \vec B_r, \vec K_r )\), \(( \vec E_2, \vec B_2, \vec K_2 )\) sont orthogonaux et directs.
Par contre, dans le milieu \((1)\) l'onde résultante \(( \vec E_1, \vec B_1 )\) n'est pas plane, car elle est la somme de l'onde incidente et de l'onde réfléchie qui ne se propagent pas selon la même direction : les plans d'ondes de ces deux ondes ne sont donc pas confondus, et ces deux ondes ne possèdent pas un même plan d'invariance.