Annexe : démonstration des relations
Démonstration : Annexe : démonstration des relations
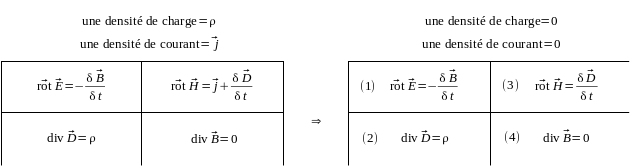
Les équations de Maxwell s'écrivent, respectivement, en un point où il y a :
\((1)\) et \((4)\) \(\Rightarrow\) \(\mathrm{div} ( \overrightarrow{\mathrm{rot}} ~ \vec E ) = 0\)
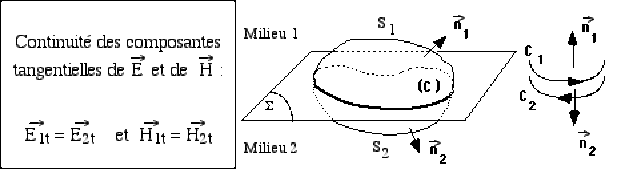
Le théorème d'Ostrogradski permet d'exprimer le flux à travers la surface fermée \((S)\) constituée de \([ S_1 \cup S_2 ]\) qui délimite le volume intérieur \(V\) :
\(\displaystyle{\oint_S ( \overrightarrow{\mathrm{rot}} ~ \vec E ) . \vec n ~ \mathrm{d}S = \int_V \mathrm{div} ( \overrightarrow{\mathrm{rot}} ~ \vec E ) ~ \mathrm{d}V}\)
\(\displaystyle{\mathrm{div} ( \overrightarrow{\mathrm{rot}} ~ \vec E ) = 0 ~~ \Rightarrow ~ \oint_S ( \overrightarrow{\mathrm{rot}} ~ \vec E ) . \vec n ~ \mathrm{d}S = 0 }\)
En exprimant ce flux à travers \((S)\) comme somme des flux à travers \(S_1\) et \(S_2\)
\(\displaystyle{\Rightarrow ~~ \int_{S_1} (\overrightarrow{\mathrm{rot}} ~ \vec E_1 ) . \vec n_1 ~ \mathrm{d}S_1 + \int_{S_2} (\overrightarrow{\mathrm{rot}} ~ \vec E_2 ) . \vec n_2 ~ \mathrm{d}S_2 = 0 ~~~~ (5)}\)
On considère les contours \(C_1\) et \(C_2\) situés infiniment près du contour \(C\) (appartenant au plan \(\sum\)), donc se confondant avec lui \((C_1 \approx C_2 \approx C)\) mais se trouvant respectivement dans les régions \(1\) et \(2\) et orientés respectivement par les normales \(\vec n_1\) et \(\vec n_2\).
Choisissant (par exemple) l'orientation de \(C\) identique à celle de \(C_1\) , on applique à \(C_1\) et \(C_2\) le Théorème de Stockes, en remarquant que :
\(\overrightarrow{\mathrm{d}l} = \overrightarrow{\mathrm{d}l}_1 = - \overrightarrow{\mathrm{d}l}_2 ~~ \Rightarrow ~ \vec E_1 . \overrightarrow{\mathrm{d}l}_1 = \vec E_{1t} . \overrightarrow{\mathrm{d}l}_1 = \vec E_{1t} . \overrightarrow{\mathrm{d}l}\) et \(\vec E_2 . \overrightarrow{\mathrm{d}l}_2 = \vec E_{2t} . \overrightarrow{\mathrm{d}l}_2 = - \vec E_{2t} . \overrightarrow{\mathrm{d}l}\)
\(\displaystyle{\int_{S_1} (\overrightarrow{\mathrm{rot}} ~ \vec E_1 ) . \vec n_1 ~ \mathrm{d}S_1 = \oint_{C_1} \vec E_1 . \overrightarrow{\mathrm{d}l}_1 = \oint_C \vec E_{1t} . \overrightarrow{\mathrm{d}l}}\)
\(\displaystyle{\int_{S_2} (\overrightarrow{\mathrm{rot}} ~ \vec E_2 ) . \vec n_2 ~ \mathrm{d}S_2 = \oint_{C_2} \vec E_2 . \overrightarrow{\mathrm{d}l}_2 = - \oint_C \vec E_{2t} . \overrightarrow{\mathrm{d}l}}\)
La relation (5) donne alors : \(\displaystyle{\oint_C \vec E_{1t} . \overrightarrow{\mathrm{d}l} - \oint_C \vec E_{2t} . \overrightarrow{\mathrm{d}l}} = 0\), soit : \(\displaystyle{\oint_C (\vec E_{1t} - \vec E_{2t}) . \overrightarrow{\mathrm{d}l} =0}\)
Cette relation étant valable quel que soit le contour \(C\) choisi dans le dioptre \(S\) de séparation des deux milieux, on a donc : \(\vec E_{1t} = \vec E_{2t}\)
En exprimant que \(\mathrm{div} (\overrightarrow{\mathrm{rot}} ~ \vec H) = 0\) [à partir des relations \((2)\) et \((3)\)] , on montre de la même façon que : \(\vec H_{1t} = \vec H_{2t}\)
Continuité des composantes normales de \(\vec B\) et de \(\vec D\) :
\(\vec B_{1n} = \vec B_{2n}\) et \(\vec D_{1n} = \vec D_{2n}\)
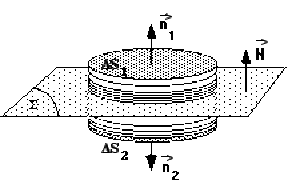
On considère la surface fermée \(S\) constituée de 2 couvercles \(\Delta S_1\) et \(\Delta S_2\), parallèles à \(S\), situés respectivement dans les milieux 1 et 2, et de la surface cylindrique s'appuyant sur ces couvercles. De plus, ces deux couvercles sont infiniment près de \(S\), et de surface suffisamment petite pour que l'on puisse considérer que la surface \(FS\) délimitée sur \(S\) par la surface latérale est telle que : \(\Delta S= \Delta S_1 = \Delta S_2\) .
Le théorème d' Ostrogradski appliqué à cette surface fermée \(S\), qui délimite un volume intérieur \(V\) donne alors, en utilisant la relation \((4)\) :
\(\displaystyle{\mathrm{div} ~ \vec B = 0 ~~ \Rightarrow ~ \oint_S \vec B . \vec n ~ \mathrm{d}S = \int_V (\mathrm{div} ~ \vec B) . \mathrm{d}V = 0}\)
La hauteur de la surface latérale étant infiniment petite, le flux de \(\vec B\) à travers cette surface latérale est négligeable par rapport aux flux respectifs à travers \(\Delta S_1\) et \(\Delta S_2\).
\(\displaystyle{\Rightarrow ~~ \int_{S_1} \vec B_1 . \vec n_1 ~ \mathrm{d}S_1 + \int_{S_2} \vec B_1 . \vec n_1 ~ \mathrm{d}S_1 \approx \oint_S \vec B . \vec n ~ \mathrm{d}S = 0}\)
Les normales étant orientées vers l'extérieur de la surface fermée, et les surfaces étant parallèles à \(S\), on a :
\(\vec n_1 = - \vec n_2 = \vec N ~~ \Rightarrow \vec B_1 . \vec n_1 = \vec B_1 . \vec N = B_{1N}\) et \(\vec B_2 . \vec n_2 = - \vec B_2 . \vec N = - B_{2N}\)
\(\displaystyle{\Rightarrow \int_{\Delta S} (B_{1N} - B_{2N}) ~ \mathrm{d}S = 0 ~~ \Rightarrow ~ B_{1N} = B_{2N}}\) soit : \(\vec B_{1N} = \vec B_{2N}\)
On montre de même [en utilisant la relation \((2)\)] : \(\vec D_{1n} = \vec D_{2n}\)