Question 2
Énoncé
A 298 K, l'enthalpie libre molaire standard de la réaction d'isomérisation :
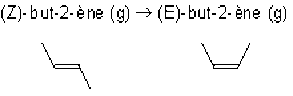
vaut 3,06 kJ.mol-1.
Déterminer la valeur de l'enthalpie libre molaire du gaz obtenu en mélangeant 0,9 mol de l'isomère Z et 0,1 mol de l'isomère E sous une pression P égale à la pression standard P°. On supposera les gaz parfaits.
Donner la réponse en kJ.mol-1.
Donnée : R = 8,314 J.mol-1.K-1.
Aide simple :
Expliciter Q, quotient réactionnel (appelé aussi monôme des activités M), en fonction des activités aE et aZ des isomères du but-ène-2.
Rappel de cours :
La formule permet de déterminer l'enthalpie libre molaire d'une réaction :
à partir de sa valeur standard () ;
des activités des espèces mises en présence.
Remarque : C'est en fait le signe de et non sa valeur absolue qu'il est important de connaître.
Le signe - indique que, pour le mélange réactionnel choisi, le sens d'évolution possible pour la réaction (1) est celui de son écriture.
Résultat
Correction
Explications
Le quotient réactionnel Q d'une réaction chimique s'exprime au moyen des activités des réactifs et des produits. Sous une forme condensée :
Le coefficient stoechiométrique est positif pour un produit, négatif pour un réactif. Pour la réaction d'isomérisation, on peut écrire :
On peut expliciter les activités. En tenant compte de l'égalité entre la pression P et la pression standard P°, et en appelant respectivement : xi, ni et nT la fraction molaire de i, la quantité de i et la quantité totale de gaz,
D'où Q = -2,38 kJ.mol-1
Application numérique : et = -2,38 kJ.mol-1
La formation de l'isomère E est donc possible.