Approche expérimentale des lois de vitesse

Relations conductivités-concentrations

La conductivité \(\chi\) d'une solution diluée d'un électrolyte fort est reliée aux conductivités équivalentes \(\lambda_i\) des espèces ioniques qu'elle contient, aux nombres de charge \(z_i\) de ces espèces et à leurs concentrations \(C_i\) :

En négligeant dans tout ce qui suit la contribution des protons (voir note^[1]), cette relation conduit aux expressions de la conductivité de la solution.

1. Au temps \(t = 0\), la conductivité est peu différente de celle d'une solution de soude 0,05 mol.L^-1 (l'ester n'est pas dissocié dans l'eau) : \(\mathbf{\chi_0=C_0.\lambda_{\textrm{Na}^+}+C_0.\lambda_{\textrm{OH}^-}}\), \(C_0\) est la concentration initiale en soude.

2. A un temps \(t\) quelconque : \(\mathbf{\chi_t=C_0.\lambda_{\textrm{Na}^+}+(C_0-C_t).\lambda_{\textrm{OH}^-}+C_t.\lambda_{\textrm{CH}_3\textrm{COO}^-}}\).

   \(C_t\) est la concentration en ions acétate \(\textrm{CH}_3\textrm{COO}^-\) formés.

   \(C_0 - C_t\) est la concentration en ions hydroxyde \(\textrm{OH}^-\) en ester \(\textrm{CH}_3\textrm{COOC}_2\textrm H_5\) restants.

3. La solution d'acétate de sodium \(\textrm{NaOAc}\) a la même conductivité que celle que l'on obtiendrait au bout d'un temps infini si la réaction était complète (l'alcool n'est pas dissocié dans l'eau) : \(\mathbf{\chi_{\textrm{CH}_3\textrm{COONa}}=C_0.\lambda_{\textrm{Na}^+}+C_0.\lambda_{\textrm{CH}_3\textrm{COO}^-}}\)

   La contribution des ions hydroxyde de cette base faible a été également négligée.

   En introduisant la conductivité initiale : il vient \(\mathbf{\chi_t=\chi_0+C_t.(\lambda_{\textrm{CH}_3\textrm{COO}^-}+\lambda_{\textrm{OH}^-})}\).

   D'où la concentration en ions acétate au temps\(t\), soit : \(\mathbf{C_t=\frac{\chi_t-\chi_0}{\lambda_{\textrm{CH}_3\textrm{COO}^-}-\lambda_{\textrm{OH}^-}}   (1)}\)

   Au bout d'un temps infini, et si la réaction était totale, la concentration en anions acétate deviendrait égale à la concentration initiale \(C_0\) en ions \(\textrm{OH}^-\). De plus, la conductivité de la solution serait égale à celle d'une solution d'acétate de sodium. La relation (1) devient donc : \(\mathbf{C_0=\frac{\chi_\textrm{NaOAc}-\chi_0}{\lambda_{\textrm{CH}_3\textrm{COO}^-}-\lambda_{\textrm{OH}^-}}    (2)}\)

   D'où la concentration en ester ou en ions hydroxyde au temps \(t\) : \(\mathbf{C_0-C_t=\frac{\chi_\textrm{NaOAc}-\chi_t}{\lambda_{\textrm{CH}_3\textrm{COO}^-}-\lambda_{\textrm{OH}^-}}   (3)}\)

   Remarque : en raison du caractère équilibré de la réaction, la valeur \(R_\infty\) de la résistance stable obtenue à partir du mélange réactionnel en attendant très longtemps diffère de \(\textrm{RNaOAc}\).

Détermination de l'ordre de la réaction

Pour obtenir la valeur de l'ordre d'une réaction chimique, on compare le comportement expérimental obtenu à ceux que l'on déduit de l'étude de modèles. On effectue cette comparaison en commençant par l'ordre le plus petit.

• Ordre 0

On suppose que les ordres partiels de la réaction d'hydrolyse par rapport à l'ester et aux ions hydroxyde sont nuls. Dans ce cas, la concentration du réactif décroît linéairement. On écrira donc, en tenant compte de la concentration en réactifs au temps \(t\) et à \(t = 0\) : \(C_0 - C_t = - k.t + C_0\) soit \(C_t = k.t\) .

La relation (1) conduit ensuite à : \(\mathbf{\chi_t=\frac{1}{R_t}=k.(\lambda_{\textrm{AcO}^-}-\lambda_{\textrm{OH}^-}).t+\chi_0}\)

Par conséquent, si la réaction d'hydrolyse était d'ordre global 0, la variation de l'inverse de la résistance en fonction du temps serait une droite de pente négative car \(\lambda_{\textrm{AcO}^-}<\lambda_{\textrm{OH}^-}\).

Ainsi que le montre la courbe ci-dessous, les points obtenus à partir des valeurs expérimentales ne s'alignent pas sur une droite.

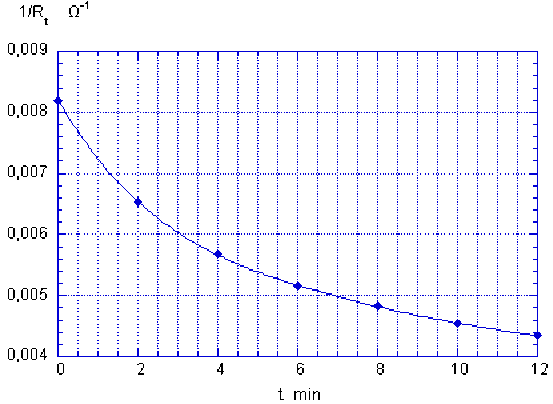
La réaction n'est donc pas d'ordre global 0.

• Ordre 1

Pour une réaction de type \(\textrm A + \textrm B\) d'ordre partiel 1 par rapport à \(\textrm A\) et d'ordre partiel 0 par rapport à \(\textrm B\), l'étude formelle montre que la variation de \(\mathbf{\ln\frac{C_0}{C_0-C_t}=f(t)}\) (où \(C\) est la concentration de l'espèce \(\textrm A\)) doit être une droite de pente \(k\).

En terme de conductivités, et en utilisant les relations (2) et (3) , cette relation s'écrit : \(\mathbf{\ln\frac{\chi_\textrm{NaOAc}-\chi_0}{\chi_\textrm{NaOAc}-\chi_t}}\) ou encore \(\mathbf{\ln\frac{(R_0-R_\textrm{NaOAc}).R_t}{(R_t-R_\textrm{NaOAc}).R_0}=k.t}\).

Les points obtenus avec cette expression sont portés sur la figure suivante :

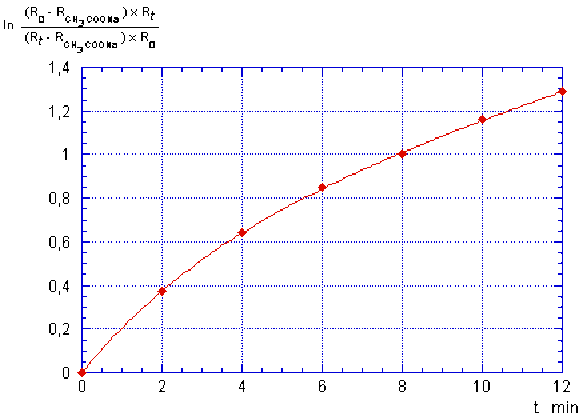
On constate que les points ne sont pas alignés, on peut donc en conclure que la réaction n'est pas du 1er ordre.

• Ordre 2

On peut supposer que la réaction est d'ordre global 2, plus précisément d'ordre partiel 1 pour chacun des réactifs. De plus, en se plaçant dans le cas particulier où les concentrations initiales des réactifs sont égales, on obtient : \(\mathbf{\frac{1}{C_0-C_t}-\frac{1}{C_0}=k.t}\) qui se réarrange en \(\mathbf{\frac{C_t}{C_0-C_t}=C_0.k.t}\).

Les relations (1) et (3) conduisent à \(\mathbf{\chi_t=\frac{\chi_0-\chi_t}{C_0.k.t}+\chi_\infty}\).

En utilisant (1), on obtient, après avoir simplifié par le facteur géométrique de la cellule :

Le graphe représentant la variation de \(\frac{1}{R_t}\) en fonction de \(\frac{\frac{1}{R_0}-\frac{1}{R_t}}{t}\) est une droite de pente \(\frac{1}{C_0.k}\).

Le traitement des résulats expérimentaux conduit au tableau :

Les points construits à partir des données des deux dernières lignes du tableau sont représentés ci-dessous :

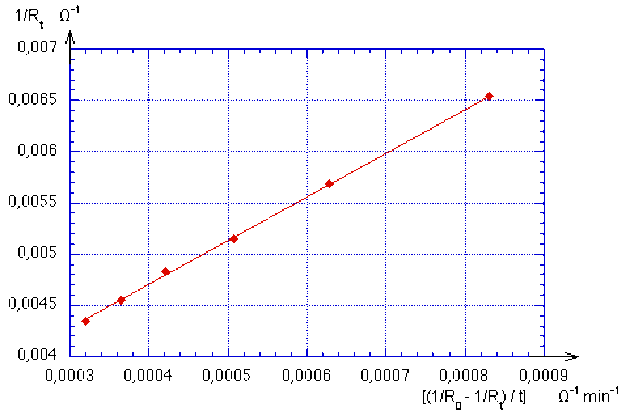
La droite qui passe par ces points a un coefficient directeur \(\frac{1}{C_0.k}\) égal à : 4,3.

D'où la valeur du coefficient de vitesse : \(\mathbf{k=\frac{1}{\textrm{4,3}\times\textrm{0,05}}=\textrm{4,7 mol}^{-1}.\textrm{L.min}^{-1}}\) .