Hydrolyse de l'acétate d'éthyle par une solution de soude
Pour déterminer les ordres partiels de la réaction par rapport à l'ester et par rapport à l'ion hydroxyde, on teste les modèles issus de l'étude formelle. Par exemple, pour une réaction d'ordre 0, on sait que la concentration de l'espèce réactif décroît linéairement dans le temps selon :
\(\mathbf{C_t=C_0-k.t}\)
Pour une réaction d'ordre partiel 1 par rapport à la base \(\textrm{OH}^-\) et d'ordre partiel 0 par rapport à l'ester, \(\mathbf{\ln\frac{C_0}{C_t}}\) est une fonction linéairement croissante de \(t\).
Pour une réaction d'ordre partiel 1 par rapport à la base \(\textrm{OH}^-\) et d'ordre partiel 1 par rapport l'ester,\(\mathbf{\frac{1}{C_t}}\) est une fonction linéairement croissante de \(t\).
Les valeurs nécessaires pour tester ces modèles ont été reportées dans le tableau :
t / min | 0 | 2 | 4 | 6 | 8 | 10 | 12 | |
|---|---|---|---|---|---|---|---|---|
Ordre 0 | Ct / (mol.L-1) | 0,0500 | 0,0320 | 0,0250 | 0,0195 | 0,0165 | 0,0140 | 0,0120 |
Ordre 1 | \(ln\frac{C_0}{C_t}\) | 0 | 0,446 | 0,693 | 0,942 | 1,109 | 1,273 | 1,427 |
Ordre 2 | (1 / Ct) / (mol-1.L) | 20 | 31,25 | 40 | 51,3 | 60,1 | 71,4 | 83,5 |
et les points correspondants sont montrées sur les figures suivantes :
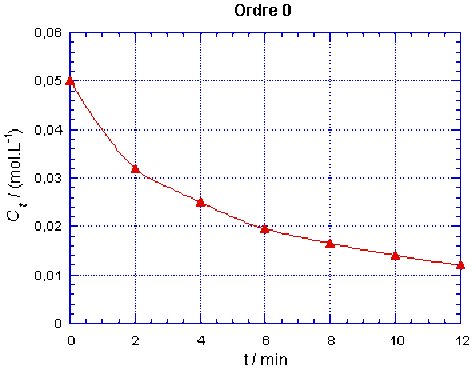
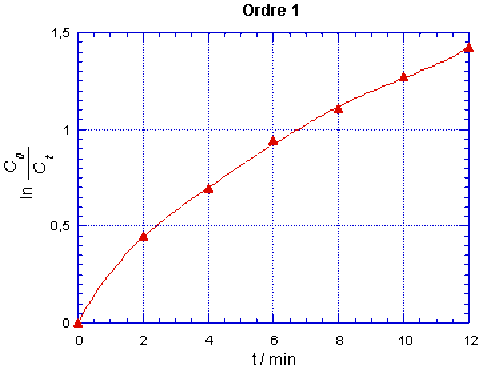
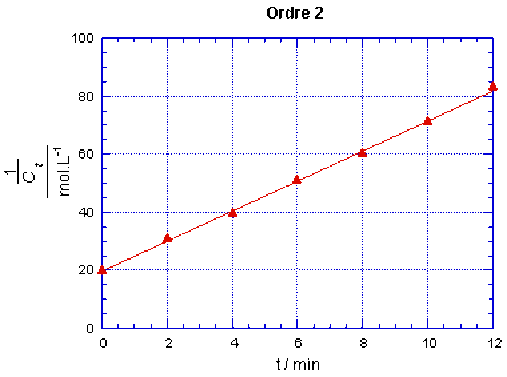
On observe que les points ne sont alignés que pour le cas correspondant à l'ordre 2. On peut alors tracer la droite qui passe par ces points, elle a pour ordonnée à l'origine \(\frac{1}{C_0} = \textrm{20,0 mol}^{-1}.\textrm L\) pour \(t = 0\). La réaction est bien d'ordre partiel 1 pour chacun des réactifs, donc d'ordre 2.
Le coefficient directeur de cette droite conduit au coefficient de vitesse de la réaction : \(\mathbf{k = \textrm{5,20 mol}^{-1}\textrm{.L.min}^{-1}}\).