Approximation dite de l'étape déterminante
Cette approximation peut s'appliquer lorsqu'il existe des réactions séries et que l'une d'entre elles a un coefficient de vitesse sensiblement inférieur à ceux des autres étapes.
Dans ces conditions, il est facile de comprendre que la vitesse globale de transformation ne peut pas être supérieure à la vitesse de la réaction la plus lente. On dit que la réaction dont le coefficient de vitesse est le plus faible impose sa vitesse. On appelle cette réaction l'étape cinétiquement déterminante ou plus simplement étape déterminante. On emploie aussi parfois le terme d'étape limitante.
Considérons par exemple le cas d'une réaction se produisant en deux étapes :
\(\mathbf{\displaystyle{\begin{array}{cccccc} \textrm A+\textrm B & \to & \textrm C & \textrm{de coefficient de vitesse} k_1\\ \textrm C & \to & \textrm D & \textrm{de coefficient de vitesse} k_2\end{array}}}\)
Il ne s'agit pas à proprement parler d'un système complexe puisqu'il est constitué seulement de deux réactions séries. Cependant, ce système est plus compliqué à étudier que celui constitué de réactions séries, toutes du premier ordre, examiné au chapitre "Réactions composées, Réactions en séries" , puisqu'ici chaque étape n'est pas du même ordre.
L'écriture des lois de vitesse sous leur forme différentielle est simple, mais leur intégration est par contre difficile.
Complément : Lois de vitesse sous leur forme différentielle
\(\mathbf{\frac{-\textrm dC_\textrm A}{\textrm dt}=\frac{-\textrm dC_\textrm B}{\textrm dt}=k_1.C_\textrm A.C_\textrm B}\)
\(\mathbf{\frac{-\textrm dC_\textrm C}{\textrm dt}=k_1.C_\textrm A.C_\textrm B-k_2.C_\textrm C}\)
\(\mathbf{\frac{-\textrm dC_\textrm D}{\textrm dt}=k_2.C_\textrm C}\)
Le déroulement de la première réaction n'est pas influencé par la seconde.
En suivant la variation de concentration des réactifs \(\textrm A\) et \(\textrm B\), on pourra vérifier que cette première réaction suit bien une loi du second ordre et déterminer la valeur de son coefficient de vitesse.
Le déroulement de la deuxième réaction dépend évidemment de la vitesse de formation de l'intermédiaire \(\textrm C\). L'étude rigoureuse nécessite l'intégration du système d'équations différentielles. Cette intégration est compliquée et conduit à des équations difficiles à exploiter.
Si les valeurs des deux coefficients de vitesse sont suffisamment différentes, on pourra appliquer l'approximation de l'étape cinétiquement déterminante.
On a donc trois cas :
\(k_1\) est beaucoup plus petit que \(k_2\)
\(k_1\) et \(k_2\) sont du même ordre de grandeur
\(k_1\) est beaucoup plus grand que \(k_2\)
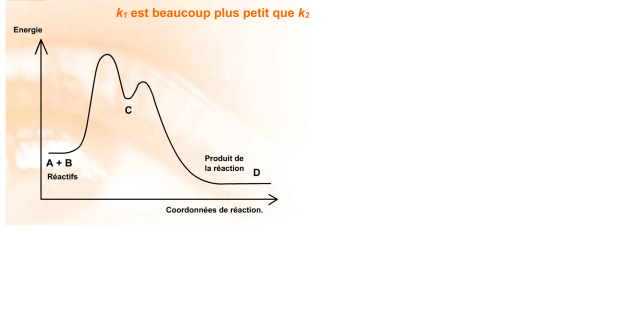
k1 est beaucoup plus petit que k2
La vitesse globale de transformation est limitée par la vitesse de la première réaction.
L'intermédiaire \(\textrm C\) ne peut pas s'accumuler, il est instantanément transformé en produit \(\textrm D\).
En fait, tout se passe comme si cet intermédiaire n'existait pas.
La réaction obéit à une loi du second ordre de coefficient de vitesse \(k_1\).
Cette situation correspond au diagramme énergétique suivant :
k1 est du même ordre de grandeur que k2
L'approximation de l'étape cinétiquement déterminante ne peut pas être appliquée. La première étape reste facile à étudier, puisqu'elle est indépendante de la seconde. L'étude de la seconde étape est plus délicate, car elle nécessite d'exploiter les équations différentielles complètes.
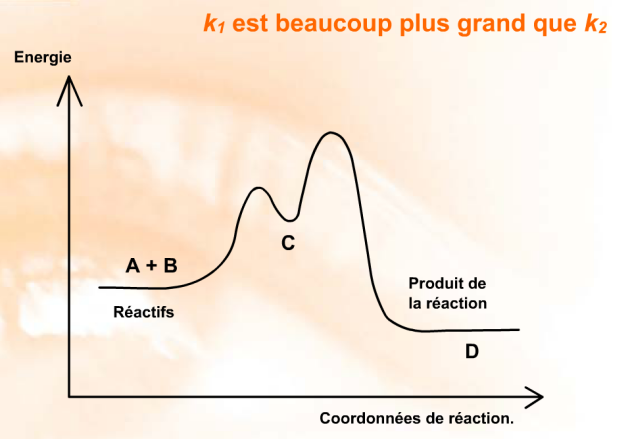
k1 est beaucoup plus grand que k2
La vitesse globale de transformation est limitée par la vitesse de la deuxième réaction.
L'intermédiaire \(\textrm C\) se forme rapidement, suivant une loi du second ordre de coefficient de vitesse \(k_1\). Puis, il va se transformer plus lentement pour donner le produit de réaction \(\textrm D\) suivant une loi du premier ordre de coefficient de vitesse \(k_2\).
La réaction se déroule donc suivant deux étapes distinctes qui correspondent à des échelles de temps différentes. La première étape est rapide et devra être observée pendant les premiers instants de la réaction. La deuxième étape est lente et devra être observée sur des temps beaucoup plus importants.
Cette situation correspond au diagramme énergétique suivant :