Diagramme potentiel-pH du chlore
Partie
Question
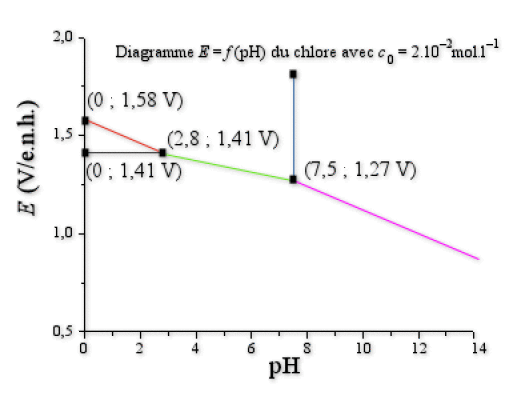
1. La figure ci-dessus représente le diagramme potentiel-\(\textrm{pH}\) du chlore en solution aqueuse en se limitant aux nombres d'oxydation -I, 0, et +I pour une concentration totale en atomes de chlore égale à \(c_0=2.10^{-2}\textrm{ mol.L}^{-1}\). Les coordonnées \((\textrm{pH} ; E)\) des points significatifs sont données sur le dessin.
a. Compléter ce diagramme en indiquant l'espèce prédominante dans chaque domaine. Les espèces sont \(\textrm{Cl}^-\), \(\textrm{ClO}^-\), \(\textrm{Cl}_2 \textrm{(aq)}\), \(\textrm{HOCl}\).
b. Ecrire la demi-réaction électrochimique relative à chaque couple.
c. Déterminer les potentiels standards des couples et \(\textrm{HOCl/Cl}_2\) et \(\textrm{HOCl/Cl}^-\).
2. Considérant les deux couples oxydo-réducteurs \(\textrm O_2 \textrm{(g)/H}_2\textrm O\) et \(\textrm H^+ \textrm{(aq)/H}_2 \textrm{(g)}\), tracer sur la figure jointe le diagramme potentiel-\(\textrm{pH}\) de l'eau en le superposant à celui du chlore. On prendra les pressions partielles des espèces gazeuses égales à 1 bar. Préciser le domaine de stabilité de l'eau sur le graphe.
3. Qu'en concluez-vous quant à la stabilité du dichlore en solution aqueuse ?
Donnée : \(E°\textrm{(O}_2 \textrm{(g)/H}_2\textrm{O)}=1\textrm,23 \textrm V/\textrm{e.n.h}\)
Solution détaillée
Remarque : tous les potentiels sont donnés par rapport à l'électrode normale à hydrogène.
1.
a. On répartit les espèces en fonction du \(\textrm{pH}\) et du degré d'oxydation (voir le cours).
Les espèces à considérer sont : \(\textrm{HOCl (DO=+I)}\), \(\textrm{ClO}^-\textrm{ (DO=+I)}\), \(\textrm{Cl}_2\textrm{ (DO=0)}\), \(\textrm{Cl}^-\textrm{ (DO=-I)}\). Notons que \(\textrm{HOCl}\) et \(\textrm{ClO}^-\) forment un couple acide/base.
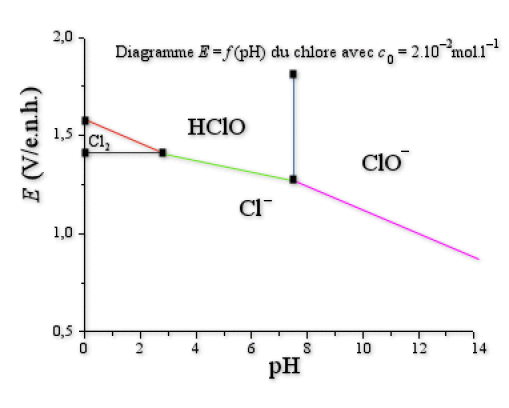
b. Demi-réactions électrochimiques :
Mis à part la droite verticale bleue (couple acide-base : échange de protons seulement), les autres droites correspondent à des équilibres rédox avec échange éventuel de protons :
(rouge) \(\textrm{(HOCl/Cl}_2\textrm) : 2.\textrm{HOCl}+2.\textrm e^-+2.\textrm H^+\to\textrm{Cl}_2 \textrm{(aq)}+2.\textrm H_2\textrm O\)
(bleu) \(\textrm{(Cl}_2 \textrm{(aq)/Cl}^-\textrm) : \textrm{Cl}_2 \textrm{(aq)}+2.\textrm e^-\to 2. \textrm{Cl}^-\)
(vert) \(\textrm{(HOCl/Cl}^-\textrm) : \textrm{HOCl}+2.\textrm e^-+\textrm H^+\to\textrm{Cl}^-+\textrm H_2\textrm O\)
(rose) \(\textrm{(ClO}^-\textrm{/Cl}^-\textrm) : \textrm{ClO}^-+2.\textrm e^-+2.\textrm H^+\to\textrm{Cl}^-+\textrm H_2\textrm O\)
c. Frontière \(\textrm{HOCl/Cl}_2\)
\(\textrm{HOCl/Cl}_2 : 2.\textrm{HOCl}+2.\textrm e^-+2.\textrm H^+\to \textrm{Cl}_2 \textrm{(aq)}+2.\textrm H_2\textrm O\)
La formule de Nernst donne ici :
\(E=E^{\circ}_{\textrm{HOCl/Cl}2}+\frac{0\textrm,06}{2}\log\frac{{[\textrm{HOCl}]^2[\textrm H^+]^2}}{[\textrm{Cl}_2 \textrm{(aq)}]}\)
A l'équilibre, c'est-à-dire sur la droite, on a égalité du nombre d'atomes de chlore présents dans \(\textrm{Cl}_2\) et dans \(\textrm{HOCl}\), soit \(2[\textrm{Cl}_2]=[\textrm{HOCl}]\). Or, il est dit dans l'énoncé que l'on travaille à concentration totale d'atomes de chlore égale à \(c_0\). Donc :
\([\textrm{HOCl}]=\frac{c_0}{2}\) et \([\textrm{Cl}_2 \textrm{(aq)}]=\frac{c_0}{4}\)
\(E=E^{\circ}_{\textrm{HOCl/Cl}2}+0\textrm,03 \log c_0[\textrm H^+]^2=E^{\circ}_{\textrm{HOCl/Cl}2}+0\textrm,03 \log c_0-0\textrm,06 \textrm{pH}\)
\(E^{\circ}_{\textrm{HOCl/Cl}2}=E-0\textrm,03 \log\textrm(2.10^{-2})+0\textrm,06 \textrm{pH}\)
Le point \((0 ;\mathrm{1,58}\textrm{ V})\) vérifie cette équation, donc on a :
\(E^{\circ}_{\textrm{HOCl/Cl}2}=1\textrm,58-0\textrm,03 \log\textrm(2.10^{-2})+0\textrm,06\times0=1\textrm,63 \textrm V\)
Frontière \(\textrm{HOCl/Cl}^-\)
\(\textrm{HOCl/Cl}^- : \textrm{HOCl}+2.\textrm e^-+\textrm H^+\to \textrm{Cl}^-+\textrm H_2\textrm O\)
\(E=E^{\circ}_{\textrm{HOCl/Cl-}}+\frac{0\textrm,06}{2}\log\frac{{[\textrm{HOCl}][\textrm H^+]}}{[\textrm{Cl}^-]}\)
Avec la convention (voir énoncé et cours) :
\([\textrm {HOCl}]=[\textrm {Cl}^-]=\frac{c_0}{2}\)
\(E=E^{\circ}_{\textrm{HOCl/Cl-}}-0\textrm,03 \textrm{pH}\)
\(E^{\circ}_{\textrm{HOCl/Cl-}}=E+0\textrm,03 \textrm{pH}\)
Le point \((2\textrm,8 \textrm; 1\textrm,41 \textrm V)\) vérifie cette équation, donc on a :
\(E^{\circ}_{\textrm{HOCl/Cl-}}=1\textrm,41+0\textrm,03\times2\textrm,8=1\textrm,49 \textrm V\)
2. les demi-équations de l'eau sont :
A/ Pour le couple \(\textrm O_2\textrm{/H}_2\textrm O\)
\((\textrm O_2\textrm{/H}_2\textrm O) : \frac12\textrm O_2+2.\textrm e^-+2.\textrm H^+\to\textrm H_2\textrm O\)
\(E=E^{\circ}_{\textrm O2\textrm{/H}2\textrm O}+\frac{0\textrm,06}{2}\log\frac{p_{\textrm O_2}[\textrm H^+]^2}{[\textrm H_2\textrm O]}\)
\([\textrm H_2\textrm O]=1\) (l'activité du solvant est généralement prise égale à 1) et, par convention (voir énoncé), \(p_{\textrm O_2}=1\textrm{ bar}\).
\(E=E^{\circ}_{\textrm O2\textrm{/H}2\textrm o}+\frac{0\textrm,06}{2}\log[\textrm H^+]=1\textrm,23-0\textrm,06 \textrm{pH}\)
B/ Pour le couple \(\textrm H^+\textrm{/H}_2\)
\((\textrm H^+\textrm{/H}_2) : 2.\textrm H^++2.\textrm e^-\to\textrm H_2\)
\(E=E^{\circ}_{\textrm H+\textrm{/H}2}+\frac{0\textrm,06}{2}\log[\textrm H^+]^2\)
La valeur de \(E^{\circ}_{\textrm H+\textrm{/H}2}\) n'est pas donnée dans l'énoncé car c'est le couple de référence en électrochimie, \(E^{\circ}_{\textrm H+\textrm{/H}2}=0 \textrm V\).
\(E=0+0\textrm,06\log[\textrm H^+]^2=-0\textrm,06 \textrm{pH}\)
On ne trace que la frontière du couple \(\textrm O_2\textrm{/H}_2\textrm O\) car le potentiel du couple \(\textrm H^+\textrm{/H}_2\) est encore plus faible et donc il n'y aura pas de réaction possible avec le proton de l'eau (voir figure suivante).
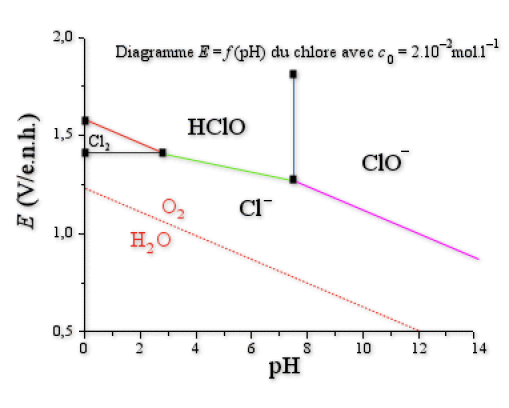
3. Le dichlore n'est pas stable en phase aqueuse : on voit bien sur le graphique que ces deux espèces n'ont pas de domaine de stabilité commun. Le dichlore est donc réduit par l'eau selon la réaction :
\(\begin{array}{c c c} (\textrm H_2\textrm O\to\frac12\textrm O_2+2.\textrm e^-+2.\textrm H^+) & \times2 \\ \textrm{Cl}_2 \textrm{(aq)}+2.\textrm e^-\to2.\textrm{Cl}^- \\ ------------ \\2.\textrm{Cl}_2 \textrm{(aq)}+2.\textrm H_2\textrm O\to 4.\textrm{Cl}^-+\textrm O_2\end{array}\)