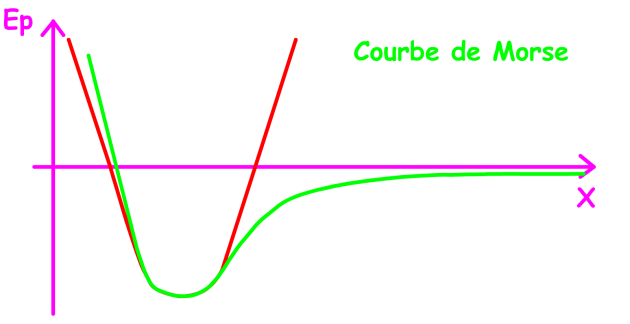
Courbe de Morse
Il se pose alors le problème de la validité du modèle de l'oscillateur harmonique pour le suivi des vibrations moléculaires.
Pour un ressort, la représentation des énergies potentielles en fonction de la longueur du ressort est une parabole dont le minimum correspond à la longueur normale du ressort. Pour une liaison, cette énergie est décrite par la courbe de Morse.
La courbe d'énergie potentielle de l'oscillateur harmonique est une parabole. Pour une molécule diatomique cette courbe d'énergie potentielle n'est pas parabolique.
Si on considère la variation d'énergie potentielle \(\textrm{Ep}\) d'une molécule diatomique en fonction de la distance X séparant les deux atomes, on observe en réalité une courbe qui présente cette forme (tracé en vert). Cette courbe est appelée courbe de Morse. Analysons la signification de cette courbe.
Considérons une molécule diatomique, par exemple, le dihydrogène

Entre les deux atomes, il peut se manifester deux types d'interaction dues à deux types de forces : forces de répulsion et d'attraction.
Si les deux atomes sont éloignés, l'énergie potentielle est quasi nulle.
Si on diminue la distance interatomique l'énergie potentielle diminue donc la stabilité augmente.
Si on diminue encore la distance interatomique, les forces de répulsion deviennent alors prépondérantes, l'énergie potentielle augmente et la stabilité décroît.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
On peut se demander ce que représente la distance \(\textrm X_0\) qui correspond au minimum d'énergie potentielle...
\(\textrm X_0\) représente la distance interatomique pour laquelle les forces d'attraction et de répulsion se compensent. C'est la position d'équilibre. Cette distance \(X_0\) correspond à ce que l'on appelle la longueur de liaison.
Remarquez que cette courbe peut s'apparenter à la parabole représentant la courbe d'énergie potentielle d'un oscillateur harmonique vers \(X_0\).
Retenons qu'au voisinage de la position d'équilibre qui correspond à la longueur de liaison, le modèle de l'oscillateur harmonique donne une bonne approximation de l'aspect énergétique d'une liaison moléculaire.
Remarque :
En résumé, le modèle de l' oscillateur harmonique est efficace tant que l'on ne s'éloigne pas trop de la distance d'équilibre, c'est-à-dire de la longueur de liaison.
D'un point de vue dynamique, il permet de calculer la "fréquence" (en fait le nombre d'onde) associée à la vibration de la liaison grâce à la relation, connue sous le nom de Loi de Hooke :
\(\mathrm{\bar \nu = \frac{1}{2.\pi.c}\sqrt{\frac{k}{\mu}}}\)
avec
k constante de force de la liaison
\(\mu\) masse réduite des deux atomes
c vitesse de la lumière
Ce nombre d'onde s'exprime en \(\mathrm{cm^{-1}}\).
L'utilisation de ce modèle permet de déduire un certain nombre de conséquences importantes au niveau moléculaire. Vous allez maintenant en voir deux.