Conséquences
Dépendance de l'ordre de la liaison
Si les deux atomes liés sont conservés et que seul l'ordre de la liaison varie, la masse réduite est constante et seul la « dureté du ressort », plus précisément la force de liaison va varier. Logiquement, si le nombre de liaisons augmente, la force de liaison augmente... donc la constante de force k augmente, et par suite la fréquence augmente ! Ainsi pour les liaisons entre carbone on pourra aisément différencier les simples, doubles et triples liaisons :
On aura la fréquence de vibration de la liaison
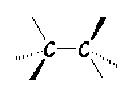
inférieure à celle de
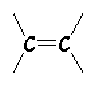
et inférieure à celle de
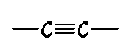
Fondamental :
Ce qu'il faut retenir : Pour un même couples d'atomes liés, plus l'ordre de liaison augmente (de simple à double puis à triple), plus la "fréquence" augmente.
Dépendance de la masse
Inversement si l'on examine des atomes simplement liés, on peut en première approximation considérer que la force de liaison varie peu comparativement à une forte variation de la masse provoquée par le remplacement de l'un des atomes par un atome d'un période différente. Reprenons la liaison \(\textrm{C-C}\) que nous venons d'étudier. Quelle sera l'évolution de la fréquence de vibration entre les deux atomes liés, si l'on remplace un des \(\textrm C\) (seconde période, masse \(12 \textrm u\)) par un \(\textrm H\) (première période, masse \(1\textrm u\)), ou par un \(\textrm{Cl }\)(troisième période, masse 35 ou \(37 \textrm u)\). Logiquement, si la masse réduite \(\mu\) augmente, comme la fréquence est inversement proportionnelle à la masse réduite \(\mu\), la fréquence d'élongation diminue. La fréquence d'élongation diminue quand la masse réduite augmente. On a par exemple :
Liaisons | Masse réduite en \(\mathrm{10^{-27}~ kg}\) | Fréquence de vibration en \(\mathrm{cm^{-1}}\) |
|---|---|---|
| 1,53 | 3030 |
| 9,95 | 1100 |
| 14,8 | 750 |
Ne mémorisez pas ces chiffres ! | ||
Ces chiffres représentent une valeur moyenne compte tenu d'autres effets structuraux qui interviennent également et que nous verrons par la suite. Il est intéressant de remarquer que la masse réduite tend globalement vers la masse du plus petit atome de la liaison
Liaisons | C-H | C-C | C-F | C-Cl | C-Br | C-I |
Masses réduites \(\mathrm {(\mu~ en 10^{-26}~ kg)}\) | 0,15 | 0,99 | 1,21 | 1,48 | 1,73 | 1,82 |
Fréquences de vibration en \(\mathrm{cm^{-1}}\) | 3030 | 1100 | 1000 | 750 | 600 | 450 |
Ne mémorisez pas ces chiffres ! | ||||||
La constante de force \(\textrm k\) variant peu pour un même type de liaison, les fréquences de vibration varient en sens inverse de \(\mu\).
Fondamental :
Ce qu'il faut retenir : Pour un même type de liaison (simple, ou double ou triple) plus la masse réduite diminue, plus la "fréquence" augmente.
Pour des liaisons comportant un même élément (\(\textrm C\)), la "fréquence" d'élongation sera la plus élevée pour la liaison associant cet élément à l'élément le plus léger de la série (\(\textrm H\)). De manière globale, la variation de la constante de force est plus faible que celle de la masse réduite \(\mu\). k ne varie au maximum que d'un facteur 4 (entre la liaison simple et la liaison triple) alors que \(\mu\) peut varier bien plus. Aussi, le facteur prépondérant pour la variation de la "fréquence" est la masse réduite \(\mu\), puis, de manière moindre, la constante de force \(\textrm k\).
Conséquences importantes : on peut découper la zone d'absorption Infra Rouge en différentes régions associées à des couples d'éléments chimiques, et aux différents types de liaisons.