Champ d'écran
Dans ce qui précède, nous avons évoqué le phénomène de Résonance Magnétique Nucléaire au niveau d'un noyau isolé. Dans ce cas, qui est celui du noyau d'hydrogène, le champ Bo subi par le noyau, est identique au champ B émis par l'aimant. La résonance est observée lorsque la fréquence \(\nu\) du champ tournant satisfait la relation \(2\pi.\nu = \gamma.Bo\)
Pour tout ce qui suit, nous utiliserons un appareillage dans lequel cette fréquence \(\nu\) est maintenue constante, et de ce fait, pour obtenir la résonance on devra agir sur le champs B émis par l'aimant pour que le noyau subisse un champ Bo.
Dans le cas particulier du noyau d'hydrogène \(\textrm H^+\), le champ subi par le noyau Bo est identique au champ émis B par l'aimant. Il n'en est pas de même lorsqu'on remplace le proton \(\textrm H^+\)+ par un atome d'hydrogène.

Dans l'atome d'hydrogène, un électron gravite autour du noyau et provoque ainsi la formation d'un champ diamagnétique Be qui s'oppose au champ émis par l'aimant B. On dit qu'il y a effet d'écran. De par la présence de ce champ diamagnétique Be, le champ subi par le noyau est inférieur au champ nécessaire à la résonance (Bo). La fréquence \(\nu\) étant maintenue constante, la condition de résonance \(2\pi.\nu = \gamma.Bo\) n'est plus satisfaite.
Pour retrouver les conditions de résonance en maintenant constante la fréquence \(\nu\), il faut augmenter l'intensité du champ B émis par l'aimant pour compenser les effets de la circulation électronique qui provoquent ce champ diamagnétique Be et retrouver l'intensité Bo nécessaire à la résonance au niveau du noyau. C'est pourquoi les spectroscopistes disent que l'atome résonne à champ plus fort que le noyau isolé ou que le signal de l'atome est blindé par rapport à celui du noyau.
Le phénomène que nous venons de décrire pour l'atome d'hydrogène isolé se retrouve lorsque l'hydrogène fait partie d'une molécule. Considérons le cas d'un alcane. La contribution des électrons de la liaison \(\textrm{C-H}\) constitue la part essentielle de l'effet d'écran sur l'atome d'hydrogène. En outre, celui-ci peut être affecté par les électrons des atomes voisins dont l'influence varie avec leur nature. Dans le cas des atomes de carbone et d'hydrogène, cette contribution à l'effet d'écran est faible.
Par contre, en substituant à un atome de carbone un atome d'oxygène, l'effet d'écran diminue. Ceci résulte de l'électronégativité de l'oxygène (\(\chi\)=3,50) supérieure à celle du carbone (\(\chi\)=2,5) (valeurs \(\chi\) de l'échelle de Pauling).
De ce fait, la densité électronique au niveau de l'atome d'hydrogène se trouve diminuée par effet inductif. Ainsi, l'effet d'écran des électrons décroît, il y a déblindage, la résonance est atteinte pour une intensité plus faible du champ B émis par l'aimant.
Inversement, la substitution d'un atome de carbone par un atome de silicium provoque un effet opposé. Le silicium est beaucoup moins électronégatif que le carbone.
électronégativité du silicium \(\chi\)=1,74
électronégativité du carbone \(\chi\)=2,5
électronégativité de l'hydrogène \(\chi\)=2,2
(valeurs \(\chi\) de l'échelle de Pauling).
De ce fait, la densité électronique augmente au niveau de l'hydrogène. Il en résulte un renforcement de l'effet d'écran. Pour retrouver la résonance, il faut augmenter l'intensité du champ B émis par l'aimant.
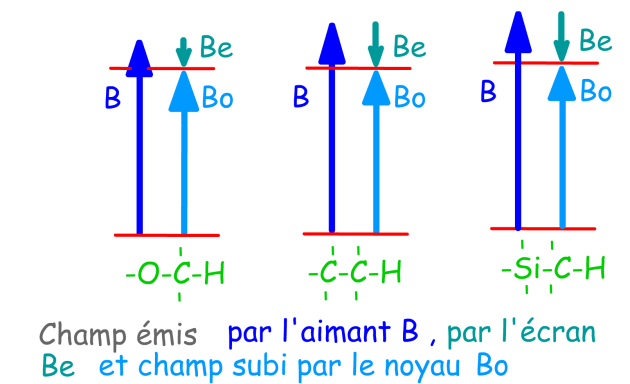
En définitive, l'intensité du champ appliqué pour atteindre la résonance traduit l'action de l'environnement électronique global sur un noyau étudié. Il apparaît ici que le champ B émis par l'aimant pour atteindre la résonance du proton \(\textrm H\) doit être plus important dans le cas d'un composé silylé que dans le cas d'un composé hydrocarboné ou oxygéné.
Cette figure résume l'influence de l'environnement d'un proton dans des conditions pour lesquelles la radiofréquence \(\nu\) de l'appareil est maintenue constante.
On observe une résonance pour le champ Bo et la relation \(2\pi.\nu = \gamma.Bo\) est satisfaite.
Réciproquement, pour des appareils dans lesquels on maintient constant le champ B émis par l'aimant, (nouvelle génération d'appareil), on observe des résonances pour des fréquences ni \(\nu_i\) différentes selon l'environnement du proton.