Cas des spins supérieurs à 1/2
Comme nous l'avons vu précédemment, ces noyaux de spin supérieur à \(\frac{1}{2}\) sont caractérisés par un moment quadrupolaire à cause de la distribution des charges électriques nucléaires qui n'est pas de symétrie sphérique comme celle que l'on observe pour les noyaux de spin \(\frac{1}{2}\) tel que le proton.
Ce moment quadrupolaire limite fortement la possibilité de perception de couplage. Cependant, pour quelques noyaux ayant un moment quadripolaire assez faible, on perçoit des couplages. C'est le cas du Deutérium \(\textrm D\) ou \(\textrm{}^2\textrm H\) et du Bore.
Vous avez vu des exemples de couplage du deutérium dans les spectres du \(\textrm{}^{13}\textrm C\) rencontrés précédemment. En effet, pour réaliser les spectres du \(\textrm{}^{13}\textrm C\) on utilise des solvants deutérés. Les solvants deutérés sont également utilisés en RMN du \(\textrm{}^1\textrm H\). En effet, les solvants hydrogénés tels que \(\textrm{Cl}_3 \textrm{CH}\),\( \textrm{CH}_3 \textrm{-CO-CH}_3\), \(\textrm{CH}_3 \textrm{-SO-CH}_3\), conduisent à un signal important en RMN du \(\textrm{}^1\textrm H\) étant donné la concentration majoritaire du solvant par rapport à celle de l'échantillon à analyser. Afin d'éviter cette "saturation" du spectre par le signal du solvant protoné, on utilise donc les solvants deutérés \(\textrm{Cl}_3 \textrm{CD}\), \(\textrm{CD}_3 \textrm{-CO-CD}_3\), \(\textrm{CD}_3 \textrm{-SO-CD}_3\). Le signal du solvant deutéré n'apparaissant plus en RMN \(\textrm{}^1\textrm H\), l'étude du spectre du composé s'en trouve nettement facilitée. Ces mêmes solvants sont utilisés en RMN du \(\textrm{}^{13}\textrm C\) pour des raisons techniques et pratiques (signal de référence ou "lock"). Ces solvants génèrent des signaux particuliers qui illustrent les couplages observés avec le deutérium.
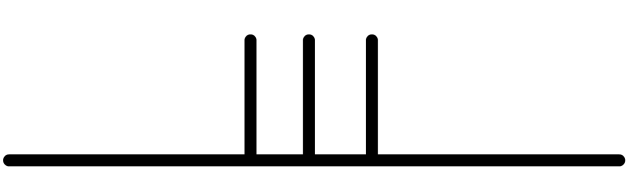
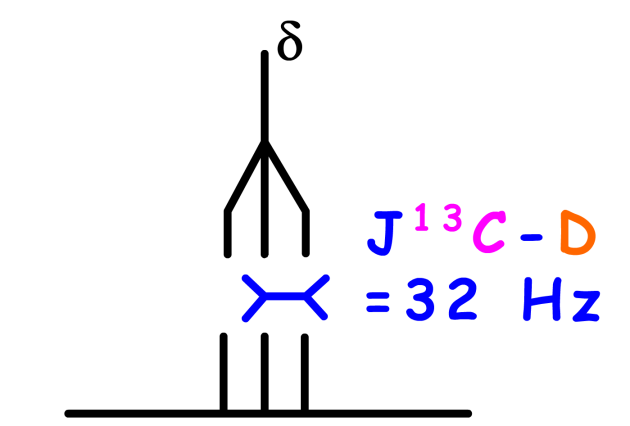
Ainsi, en RMN du \(\textrm{}^{13}\textrm C\), tous les spectres réalisés dans le \(\textrm{CDCl}_3\) présentent trois raies de même intensité vers 77 ppm
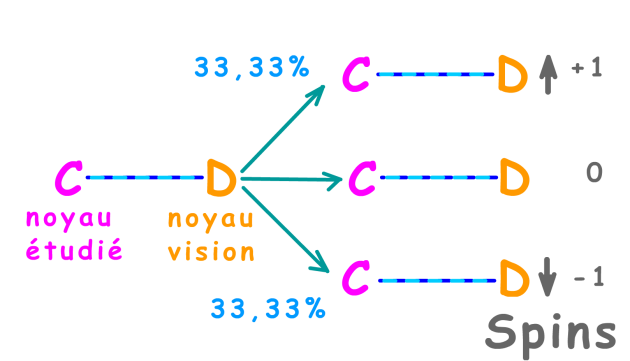
Le deutérium a un spin égal à 1. De ce fait, il présente trois états magnétiques possibles. Dans l'état fondamental, le noyau de deutérium a autant de chances de présenter un spin +1 que de présenter un spin 0 ou -1.
Lorsqu'il est soumis aux effets d'un seul deutérium voisin, le \(\textrm{}^{13}\textrm C\) étudié peut donc se trouver dans trois situations d'égale probabilité. Il peut percevoir le deutérium voisin dans l'état de spin m = +1, ou dans l'état de spin m = 0, ou dans l'état de spin m = -1.
Ainsi, la raie centrale correspond à m = 0, les deux autres raies latérales aux états +1 et -1. En RMN du \(\textrm{}^{13}\textrm C\), le signal observé pour le \(\textrm{Cl}_3\textrm{C-D}\) est donc un triplet d'égale intensité du fait de l'égalité des probabilités de présence des trois états de spin du deutérium.
Pour le diméthylesulfoxyde deutéré \(\textrm{CD}_3\textrm{-SO-CD}_3\)3, le signal observé RMN du \(\textrm{}^{13}\textrm C\) est plus complexe...
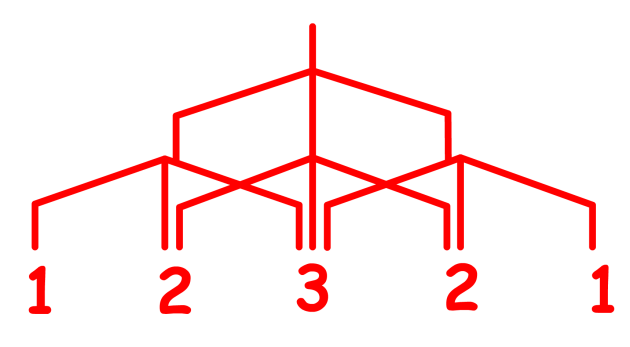
Dans ce cas, le \(\textrm{}^{13}\textrm C\) étudié voit cette fois-ci 3 deutériums...
Chaque raie du triplet d'égale intensité va être détriplée deux fois. Vu l'égalité des constantes de couplage qui entraîne des superpositions de raies, c'est un ensemble de 7 raies que l'on va observer pour \(\textrm{CD}_3\textrm{-SO-CD}_3\) en RMN du \(\textrm{}^{13}\textrm C\) (avec \(J^{13}\textrm C-D\) = 25 Hz).
Pour n couplages identiques avec un noyau de spin I, on observera donc 2nI+1 raies... dans le cas du proton I=1/2... et on avait n+1 raies...
EtOH avec du DMSO deutéré \(\textrm{CH}_3\textrm{-CH}_2\textrm{-OH}\) + \(\textrm{CD}_3\textrm{-SO-CD}_3\)
Une explication à propos des cinq raies observées pour le Diméthylsulfoxyde deutéré dans le spectre de l'éthanol... S'il s'agissait du \(\textrm{CD}_3\textrm{-SO-CD}_3\) pur on ne devrait pas observer de raie pour ce solvant en RMN du \(\textrm{}^1\textrm H\) !
En fait, on n'utilise pas de DMSO deutéré absolument pur... cela coûte trop cher...
Le DMSO utilisé contient toujours du \(\textrm{CD}_2\textrm{H-SO-CD}_3\)... à l'état d'impureté et on le voit en RMN du \(\textrm{}^1\textrm H\) ! Le proton \(\textrm H\) subit le couplage des deux atomes de deutérium voisins. On obtient donc 2nI+1 = 2*2*1+1 = 5 raies. Le signal observé n'est donc pas celui du DMSO hexadeutéré ! En général, dans tous les spectres réalisés en prèsence du DMSO deutéré on observera ce signal de l'impureté... le DMSO pentadeutéré.
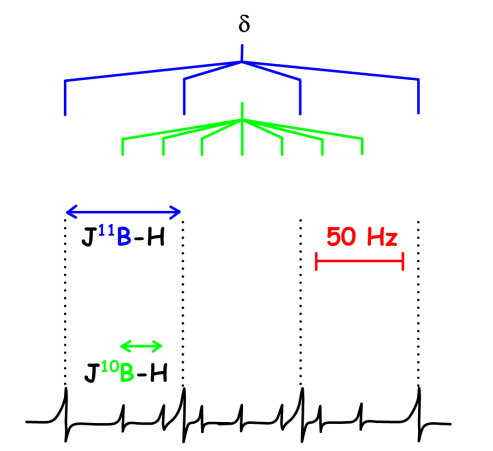
Examinons le spectre de \(\textrm{NaBH}_4\) en RMN du proton \(\textrm{}^1\textrm H\). On peut s'attendre à observer un seul déplacement chimique... mais quelle sera la multiplicité du signal ?
Il faut savoir que le Bore présente deux isotopes : \(\textrm{}^{11}\textrm{B}\) de spin I=3/2 présent à 81 % et \(\textrm{}^{10}\textrm{B}\) de spin I=3 présent à 19 %. Donc si on applique la règle des 2nI+1 raies :
pour \(\textrm{}^{11}\textrm{BH}_4\textrm-\) on aura 2*1*3/2 +1 = 4 raies correspondant à m=-3/2,-1/2,+1/2,+3/2
pour \(\textrm{}^{10}\textrm{BH}_4\textrm-\) on aura 2*1*3 +1 = 7 raies correspondant à m=-3,-2,-1,0,+1,+2,+3.
D'un point de vue intensité des raies, elle est reliée à l'abondance isotopique. Les quatres grandes raies représentent 81 % du signal et les sept petites autres, uniquement 19 % du signal.