Le théorème du moment cinétique
On peut ici faire l'analogie avec le théorème du moment cinétique pour les systèmes à force centrale en mécanique classique ; selon ce théorème le vecteur moment cinétique est une constante.
\(\mathbf{\overrightarrow l=\overrightarrow r\land m.\overrightarrow v}\) est une constante en mécanique classique
Ce vecteur moment cinétique est illustré ci contre :
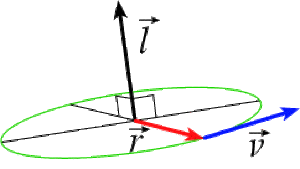
En mécanique quantique, l'analogue du théorème du moment cinétique indique que dans un état quantique \(\Psi_{\mathrm{n l m}}\), le module au carré du moment cinétique et sa projection sur l'axe \(\textrm Oz\) sont des constantes du mouvement :
\(\mathbf{\overrightarrow l^2}\) et \(\mathbf{l_z}\) sont des invariants du mouvement en mécanique quantique
Les composantes \(l_x\) et \(l_y\) ne sont pas des invariants.
On doit donc considérer, si on veut se représenter le vecteur moment cinétique associé à une orbitale \(\Psi_{\mathrm{n m l}}\) , que celui-ci se positionne sur un cône de hauteur \(\mathrm{l_z}\) constante, appelé cône de précession.
