Application de la relation de Bragg
Partie
Question
On envoie un faisceau de rayons X de longueur d'onde \(\lambda=1,54\AA\) sur un cristal d'aluminium de structure cfc. Le paramètre de maille vaut \(\mathrm{a=4,04\AA}\).
Calculer la valeur de l'angle de diffraction pour laquelle on observe une réflexion de premier ordre correspondant à la plus petite distance réticulaire entre plans parallèles à une face.
Aide simple
La relation de Bragg s'écrit :
\(2\mathrm{~d~\sin\theta=k~\lambda}\)
où d est la distance réticulaire, \(\lambda\) est la longueur d'onde d'irradiation, \(\theta\) est l'angle de diffraction et k est l'ordre.
Au premier ordre, k = 1.
Aide méthodologique
Dans cet exercice, il faut d'abord identifier la famille de plans qui diffractent. On s'aidera d'un dessin.
On peut alors relier la distance réticulaire au paramètre de maille pour pouvoir appliquer la relation de Bragg.
Solution détaillée
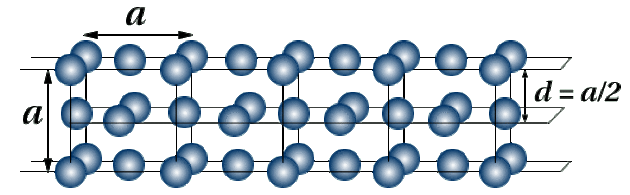
On a représenté ci-dessous l'arrangement des plans réticulaires d'un réseau cfc.
La plus petite distance correspond à \(\mathrm{d=\frac{a}{2}}\).
On applique la relation de Bragg au premier ordre :
\(2\mathrm{~d~\sin\theta=k~\lambda}\) avec \(\mathrm{k}=1\)
\(\sin\theta=\frac{\lambda}{2~\mathrm{d}}=\frac{1,54}{4,04}=0,381\)
L'ange de diffraction vaut \(\theta=22,41°\)