Résumé : Action sur une matrice du produit par des matrices élémentaires
On a une description complète des transformations élémentaires sur les matrices en termes de produit de matrices soit par une matrice élémentaire, d'un côté ou de l'autre, soit par un produit de quatre matrices élémentaires (égale à une matrice d'échange).
Il faut noter que les transformations élémentaires sur les colonnes d'une matrice à \(n\) lignes et \(p\) colonnes proviennent du produit à droite de cette matrice par des matrices élémentaires d'ordre \(p\) et que celles sur les lignes proviennent du produit à gauche de cette matrice par des matrices élémentaires d'ordre \(n\).
Plus précisément, on a les résultats suivants :
Soit\( n \textrm{ et }p\) deux entiers supérieurs ou égaux à \(2\). Soit \(\mathcal M\in\mathcal M_{n,p}(\mathcal K)\). On note \(\mathcal C_s\) (respectivement \(\mathcal L_t\)) les colonnes (respectivement les lignes) de la matrice \(\mathcal M\).
Transformation sur les colonnes
Soient i et j deux entiers distincts compris entre \(1\) et \(p\) et \(\lambda\) un élément quelconque de \(\mathbf K\).
On considère la matrice d'ordre \(p\), \(\mathcal T_{i,j}(\lambda)\).
La matrice qui a les mêmes colonnes que \(\mathcal M\) sauf éventuellement la j-ième qui est égale à \(\mathcal C_j+\lambda\mathcal C_i\) , est la matrice\( \mathcal M\mathcal T_{i,j}(\lambda)\).
Soient i un entier compris entre \(1\) et \(p\) et\( \lambda\) un élément non nul de \(\mathbf K\). On considère la matrice d'ordre \(p\), \(\mathcal D_i(\lambda)\).
La matrice qui a les mêmes colonnes que \(\mathcal M\) sauf éventuellement la i-ième qui est égale à est \(\lambda\mathcal C_i\) est la matrice \(\mathcal M\mathcal D_i(\lambda)\).
Définition : Définition des matrices élémentaires
Soit \(n\) un entier supérieur ou égal à \(2\). Soient deux entiers distincts \(i \textrm{ et }j\), compris entre \(1 \textrm{ et }n\), et un élément de \(\mathbf K\).
On définit la matrice \(\mathcal T_{i,j}(\lambda)\in\mathcal M_{n}\mathbf K\) par
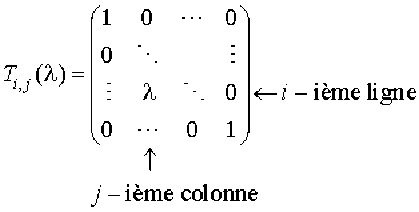
Les éléments de la diagonale principale sont tous égaux à \(1\), \(\lambda\) se trouve à la i-ième ligne et j-ième colonne et tous les autres éléments sont nuls.
Soit \(\lambda\) un élément non nul de \(\mathbf K\).
On définit la matrice diagonale \(\mathcal D_i(\lambda)\in\mathcal M_n(\mathbf K)\) par :
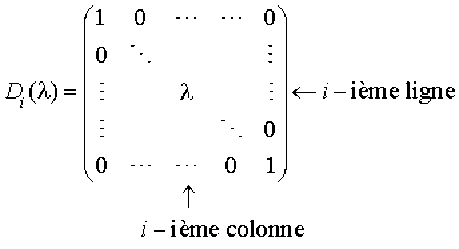
\(\lambda\) se trouve à la i-ième ligne et i-ième colonne, tous les autres éléments de la diagonale principale sont égaux à \(1\).
Soient\( i\) et \(j\) deux entiers distincts compris entre \(1\) et \(p\). On considère la matrice \(\Delta_{i,j}\), d'ordre p.
Alors la matrice obtenue à partir de \(\mathcal M\) en échangeant les colonnes i et j de \(\mathcal M\) est égale à \(\mathcal M\Delta_{i,j}\).
Description des matrices Delta i,j
C'est une matrice symétrique et elle vérifie, pour tout\( i\) et \(j\) entiers compris entre \(1\) et \(k\), l'égalité \(\Delta_{i,j}=\Delta_{j,i}\)
De plus on a démontré la formule
\(\Delta_{i,j}=\mathcal T_{i,j}(1)\mathcal T_{j,i}(-1)\mathcal T_{i,j}(1)\mathcal D_i(1)\). Les matrices élémentaires intervenant dans cette formule ont le même ordre que \(\Delta_{i,j}\).
Transformations sur les lignes
Soient\( i\) et \(j\) deux entiers distincts compris entre \(1\) et \(n\) et \(\lambda\) un élément quelconque de \(\mathbf K\).
On considère la matrice d'ordre \(n\),\(\mathcal T_{i,j}(\lambda)\) .
La matrice qui a les mêmes lignes que\( \mathcal M\) sauf éventuellement la i-ième qui est égale \(\mathcal L_i+\lambda\mathcal L_j\) à est la matrice \(\mathcal T_{i,j}(\lambda)\mathcal M\).
Soient \(i\) un entier compris entre \(1\) et \(n\), un élément non nul de \(\mathbf K\). On considère la matrice d'ordre \(n\) , \(\mathcal D_i(\lambda)\).
La matrice qui a les mêmes lignes que \(\mathcal M\) sauf éventuellement la i-ième qui est égale à est \(\lambda\mathcal L_i\) est la matrice \(\mathcal D_i(\lambda)\mathcal M\)
Soient i et j deux entiers distincts compris entre \(1\) et \(n\) et la matrice d'ordre \(n\), \(\Delta_{i,j}\).
Alors la matrice obtenue à partir de \(\mathcal M\) en échangeant les lignes i et j de \(\mathcal M\) est égale à \(\Delta_{i,j}\mathcal M\)