Bilan
On peut résumer les propriétés précédentes.
Pour la série à termes complexes \(\sum a_nz^n\)
Soit \(\sum a_nz^n\) une série entière de rayon de convergence \(R\) et soit \(z_0\in C\).
Si \(z_0\) appartient au disque de convergence \(D(0,R)\), (c'est-à-dire \(|z_0|<R\)), la série \(\sum a_nz^n_0\) est absolument convergente.
Si \(z_0\) est extérieur au disque fermé \(\overline{D}(0,R)\), (c'est-à-dire \(|z_0|>R\)), la série \(\sum a_nz^n_0\)est divergente.
Si \(z_0\) appartient au cercle \(C(0,R)=\{z\in C, |z|= R\}\), on ne peut rien dire a priori sur la série \(\sum a_nz^n_0\).
Remarque :
Ainsi le disque de convergence \(D(0,R)\)d'une série entière \(\sum a_nz^n\) n'est pas toujours le plus grand ensemble de \(C\) sur lequel la série \(\sum a_nz^n\) est convergente.
Pourquoi ?
Parce qu'il faut regarder ce qui se passe sur le cercle \(C(0,R)\).
Sur le cercle \(C(0,R)\) la série \(\sum a_nz^n\) peut être
convergente en tout point,
convergente en certains points,
divergente en tout point.
Dans le premier cas, le plus grand ensemble de convergence de la série \(\sum a_nz^n\) est le disque fermé \(\overline{D}(0,R)\). Nous verrons des exemples au paragraphe suivant.
Pour la série entière \(\sum a_nz^n\)
Soit \(\sum a_nz^n\) une série entière de rayon de convergence \(R\).
La série entière \(\sum a_nz^n\) est normalement donc uniformément convergente dans tout disque fermé \(\overline{D}(0,\rho)\) avec \(\rho<R\).
En général, la série entière \(\sum a_nz^n\) n'est pas uniformément convergente dans le disque de convergence, ni a fortiori dans le disque fermé \(\overline{D}(0,R)\).
Remarque :
Quand la série \(\sum a_nz^n\) est convergente dans le disque fermé \(\overline{D}(0,R)\), il peut arriver que la série entière soit uniformément convergente dans le disque fermé \(\overline{D}(0,R)\). Nous en verrons des exemples plus loin.
Convergence/divergence
La série est divergente à l'extérieur du disque

Convergence uniforme
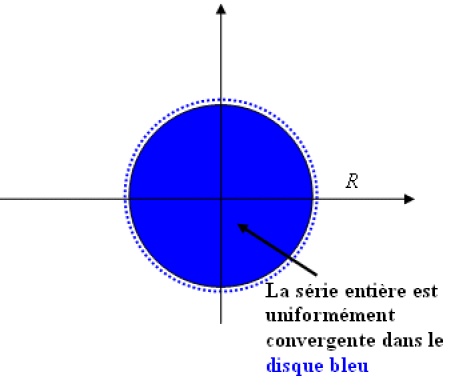
Attention, le disque bleu a un rayon strictement inférieur à R.