Analyse des réseaux linéaires

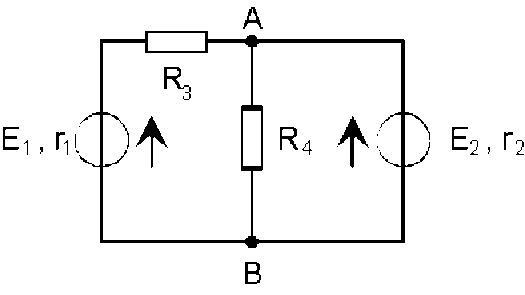
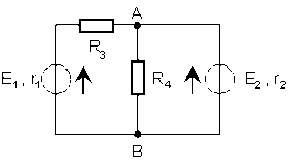
Dans le réseau ci-dessus, pour calculer l'intensité du courant traversant l'élément de résistance \(R_4\), on peut procéder en deux étapes :

• calculer les caractéristiques du générateur de courant équivalent au réseau (dans lequel on a enlevé la branche contenant l'élément de résistance \(R_4\) ) "vu de \(A \textrm{ et }B\)"

• remplacer le réseau par le générateur pour calculer le courant traversant l'élément de résistance \(R_4\)

Première étape :

• calcul du courant de court-circuit :

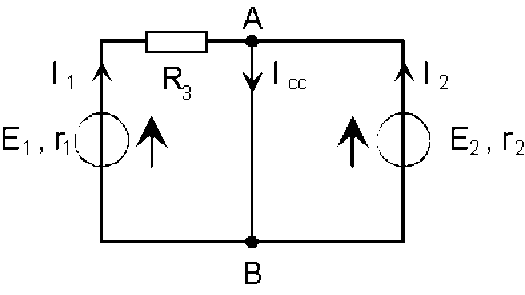
puisqu'il y a court-circuit, on peut écrire :

\(\begin{array}{lll}V_A-V_B & = & 0\\& = & E_1-(r_1+R_3).I_1\\& = & E_2-r_2.I_2\end{array}\)

d'où :

\(\displaystyle{I_1= \frac{E_1}{r_1+R_3}\textrm{ ; }I_2=\frac{E_2}{r_2}\textrm{ ; }I_{cc}=I_1+I_2=\frac{E_1}{r_1+R_3}+\frac{E_2}{r_2}}\)

soit : \(\displaystyle{I_{cc}=I_1+I_2=\frac{r_2.E_1+(r_1+R_3).E_2}{r_2(r_1+R_3)}}\)

et, en utilisant les conductances :

\(\displaystyle{I_{cc}=\frac{g_1G_3}{g_1+G_3}E_1+g_2E_2=\frac{g_1G_3E_1+g_2(g_1+G_3)E_2}{g_1+G_3}}\)

• calcul de la conductance du réseau vu de \(A \textrm{ et }B\) :

on remplace les générateurs par leur résistance interne; vu des nœuds \(A \textrm{ et }B\), le réseau est formé de deux branches en parallèle, d'où sa conductance :

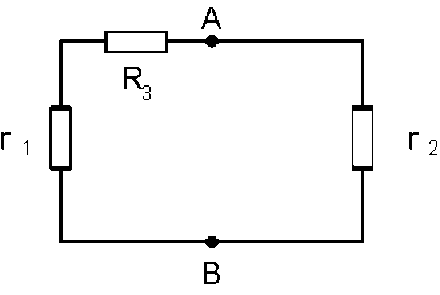
\(\displaystyle{G_{AB}=g_2+\frac{g_1G_3}{g_1+G_3}=\frac{g_1g_2+g_2G_3+G_3g_1}{g_1+G_3}}\)

Deuxième étape:

• calcul du courant traversant l'élément de résistance \(R_4\) :

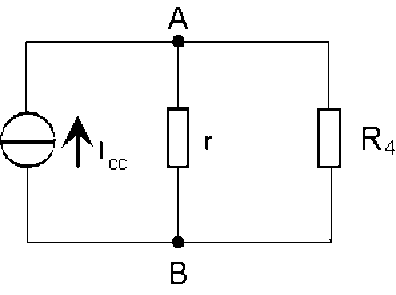
on remplace le réseau par un générateur de courant, débitant un courant maximum \(I_{cc}\), et de conductance interne \(g = G_{AB}\); l'ensemble \((r, R_4)\) constitue un diviseur de courant^[3] ; d'où l'intensité du courant :

\(\displaystyle{I_4=I_{cc}\frac{G_4}{G_{AB}+G_4}}\) \(=\displaystyle{I_{cc}\frac{G_4(g_1+G_3)}{g_1g_2+g_1G_3+g_2G_3+g_1G_4+G_3G_4}}\)

En remplaçant \(I_{cc}\) par son expression en fonction de \(E_1\) et \(E_2\) :

\(\displaystyle{{I}_{{4}}=\frac{{{g}_{{1}}{G}_{{3}}{E}_{{1}}+{g}_{{2}}{\left({g}_{{1}}+{G}_{{3}}\right)}{E}_{{2}}}}{{{g}_{{1}}+{G}_{{3}}}}}\).\(\displaystyle{\frac{{{G}_{{4}}{\left({g}_{{1}}+{G}_{{3}}\right)}}}{{{g}_{{1}}{g}_{{2}}+{g}_{{1}}{G}_{{3}}+{g}_{{2}}{G}_{{3}}+{g}_{{1}}{G}_{{4}}+{G}_{{3}}{G}_{{4}}}}}\)

\(=\displaystyle{{G}_{{4}}\frac{{{g}_{{1}}{G}_{{3}}{E}_{{1}}+{g}_{{2}}{\left({g}_{{1}}+{G}_{{3}}\right)}{E}_{{2}}}}{{{g}_{{1}}{g}_{{2}}+{g}_{{1}}{G}_{{3}}+{g}_{{2}}{G}_{{3}}+{g}_{{1}}{G}_{{4}}+{G}_{{3}}{G}_{{4}}}}}\)

Et, en remplaçant les conductances par leurs expressions en fonction des résistances, on obtient, comme pour les autres méthodes :

\(I_{4} = \frac{r_{2}E_{1} + (r_{1}+R_{3})E_{2}}{r_{1}r_{2} + r_{1}R_{4} + r_{2}R_{3} + r_{1}R_{4} + R_{3}R_{4}}\)

\(\qquad\)

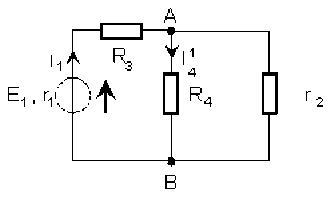
Dans un premier temps, on ne conserve que le générateur placé dans la branche de gauche, et on remplace l'autre par sa résistance interne \(r_2\), ce qui donne le montage ci-dessus.

Le courant débité par le générateur est :

\(\begin{array}{lll}I_1 & = & \frac{E_1}{r_1+R_3+\frac{r_2R_4}{R_2+R_4}}\\\\& = & \frac{E_1(r_2+R_4)}{(r_2+R_4)(r_1+R_3)+r_2R_4}\end{array}\)

L'ensemble (\(r_2\), \(R_4\)) constitue un diviseur de courant^[3]. Le courant dans \(R_4\) a donc pour intensité :

\(\displaystyle{I_4^1=I_1 \frac{r_2}{r_2+R_4}= \frac{E_1.r_2}{(r_2+R_4)(r_1+R_3)+r_2R_4}}\)

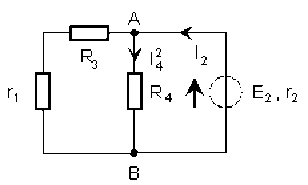
Dans un second temps, on ne conserve que le générateur placé dans la branche de droite, et on remplace l'autre par sa résistance interne \(r_1\), ce qui donne le montage ci dessus.

Le courant débité par le générateur est :

\(\begin{array}{lll}I_2 & = & \frac{E_2}{r_2+\frac{(r_1+R_3).R_4}{r_1+R_3+R_4}}\\\\& = &\frac{E_2.(r_1+R_3+R_4)}{r_2.(r_1+R_3+R_4)+(r_1+R_3).R_4}\end{array}\)

L'ensemble (\(r_1+R_3\), \(R_4\)) constitue un diviseur de courant. Le courant dans \(R_4\) a donc pour intensité :

\(\displaystyle{I_4^2=I_2\frac{r_1+R_3}{r_1+R_3+R_4} = \frac{E_2.(r_1+R_3)}{r_2.(r_1+R_3+R_4)+(r_1+R_3).R_4}}\)

Le courant qui traverse \(R_4\) dans le réseau de départ a donc pour intensité :

\(\displaystyle{I_4=I_4^1+I_4^2=\frac{E_1.r_2+E_2.(r_1+R_3)}{r_1r_2+r_1R_4+r_2R_3+r_2R_4+R_3R_4}}\)

résultat que l'on peut retrouver en utilisant, par exemple, les lois de Kirchhoff :

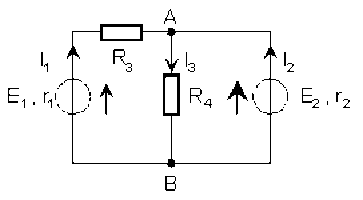
Le réseau comporte deux nœuds et trois branches, il y a donc deux mailles indépendantes. Le squelette doit joindre tous les nœuds: on peut prendre comme squelette n'importe laquelle des trois branches. Puisqu'on veut calculer l'intensité du courant dans la branche contenant \(R_4\), il vaut mieux choisir pour squelette une autre branche, par exemple celle de gauche. Les inconnues seront donc les intensités des courants circulant dans la branche centrale et dans celle de droite.

Appelons les \(I_4\) et \(I_2\). L'intensité \(I_3\) du courant débité par le générateur de gauche est donnée par la loi aux nœuds :

\(I_4 = I_2 +I_3\)

\(I_3 = I_4 -I_2\)

Le long de la maille formée par le squelette et la branche centrale, on a :

\(E_1 - r_1 .I_3 - R_3 .I_3 - R_4 . I_4 = 0\)

En remplaçant dans cette équation \(I_3\) par son expression en fonction de \(I_2\) et de \(I_4\), il vient :

\(E_1-(r_1+R_3)(I_4-I_2)-R_4I_4= 0\)

et, après le regroupement des termes :

\(-(r_1+R_3)I_2+(r_1+R_3+R_4)I_4=E_1 (1)\)

Le long de la maille formée par la branche centrale et la branche de droite, on a :

\(E_2-r_2I_2-R_4I_4=0\)

L'intensité \(I_4\) est donc solution d'un système de deux équations a deux inconnues :

\(- (r_1+R_3)I_2+(r_1+R_3+R_4)I_4=E_1 (1)\)

\(r_2I_2-R_4I_4=E_2 (2)\)

La deuxième équation permet d'exprimer simplement \(I_2\) en fonction de \(I_4\)

\(I_2=\frac{E_2}{r_2}+\frac{R_4}{r_2}I_4\)

Le report de cette expression dans (1) donne :

\(\displaystyle{-(r_1+R_3)\bigg(\frac{E_2}{r_2}+\frac{R_4}{r_2}I_4\bigg)+(r_1+R_3+R_4)I_4=E_1}\)

d'où finalement :

\(\displaystyle{I_4=\frac{E_1.r_2+E_2(r_1+R_3)}{r_1r_2+r_1R_4+r_2R_3+r_2R_4+R_3R_4}}\)