Equivalence Thévenin-Norton
Durée : 4 mn
Note maximale : 2
Question
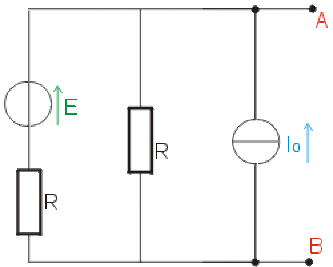

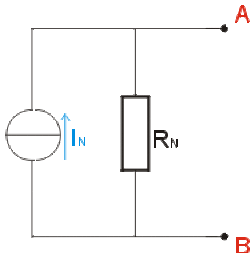
A la question précédente, la transformation de Norton a montré l'équivalence des deux schémas ci-dessus,
avec \(\displaystyle{ I_N = \frac{E}{R} + I_0 }\) ; \(\displaystyle{ R_N = \frac{R}{2} }\)
Trouver le générateur de Thévenin équivalent.
Solution

\(E_T=R_N . I_N\)
\(\displaystyle{ I_N = \frac{E}{R} + I_0 }\)
\(\displaystyle{ R_N = \frac{R}{2} }\)
\(\displaystyle{ E_T = \frac{R}{2} \left( \frac{E}{R} + I_0 \right) = \frac{E}{2} + \frac{R . I_0}{2} }\) (1 pt)
\(\displaystyle{ R_T = R_N = \frac{R}{2} }\) (1 pt)