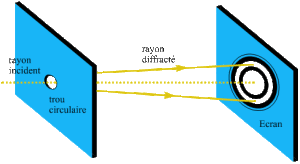
Intensité diffractée à l'infini par une ouverture circulaire éclairée sous incidence normale par un faisceau de lumière monochromatique
Dans la pratique, les instruments d'optique utilisent des miroirs ou des lentilles limités par des diaphragmes circulaires qui introduisent donc des phénomènes de diffraction par des ouvertures circulaires. Ceux-ci ont l'inconvénient de limiter le pouvoir de résolution des instruments d'optique.
Calculons l'intensité diffractée à l'infini par une ouverture circulaire éclairée sous incidence normale par un faisceau de lumière monochromatique.
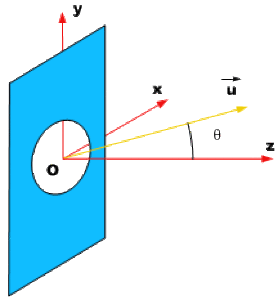
Le problème est de symétrie de révolution autour de l'axe \(Oz\) du diaphragme de rayon \(R\). La figure diffractée aura la même symétrie. Considérons donc une direction caractérisée par l'angle \(\theta\) que fait un rayon diffracté avec l'axe \(Oz\).
En utilisant les coordonnées cylindriques et en prenant \(\vec u\) dans le plan \(Ox,Oz\) pour simplifier les calculs, on a :
\(\vec u = \cos \theta ~.~ \vec e_z ~+~ \sin \theta ~.~ \vec e_x\)
L'amplitude de la vibration diffractée dans la direction \(\vec u\) par un élément de surface \(\mathrm d^2 S\) centré sur \(M\) s'écrit :
\(\mathrm d A = A_0 ~.~ \mathrm d^2 S ~.~ \mathrm e^{i ~ 2 \pi ~ \varphi}\)
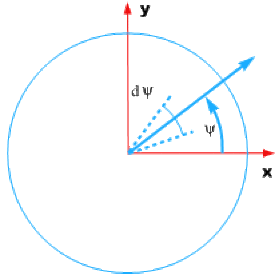
En coordonnées cylindriques on aura :
\(\mathrm d^2 S = \mathrm d r ~.~ \mathrm d \psi ~.~ r\)
avec :
\(0 \le r \le R\)
\(0 \le \psi \le 2 \pi\)
D'autre part :
\(\varphi = 2 \pi \frac{\delta}{\lambda}\)
et
\(\delta = \overrightarrow{OM} ~.~ \vec u\)
\(\overrightarrow{OM} = ( \cos \psi ~.~ \vec e_x ~+~ \sin \psi ~.~ \vec e_y) ~.~ r\)
et
\(\delta = r ~.~ \cos \psi ~.~ \sin \theta\)
d'où
\(\displaystyle{A = \int_0^{2 \pi} \int_0^R A_0 ~ e^{i \frac{2 \pi}{\lambda} r . \cos \psi . \sin \theta} r ~ \mathrm d r ~\mathrm d \psi}\)
et l'éclairement en un point \(P\) est proportionnel à : \(I = A . A^{\ast}\)
Le calcul se fait en introduisant la première fonction de Bessel dont les résultats permettent de tracer I/I_0 en fonction de \sin \theta : \frac{I}{I_0} = \Big( 2 \frac{\mathrm J_1 (m)}{m} \Big)^2
m | \(\frac{I}{I_0}\) | |
|---|---|---|
Maximum central | 0 | 1 |
1er minimum | 3,832 | 0 |
1er maximum | 5,136 | 002 |
2ème minimum | 7,015 | 0 |
2ème maximum | 8,417 | 0 |
3ème minimum | 10,173 | 0 |
3ème maximum | 11,620 | 0 |
4ème minimum | 13,324 | 0 |
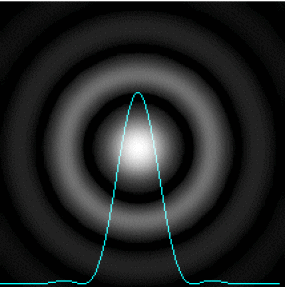
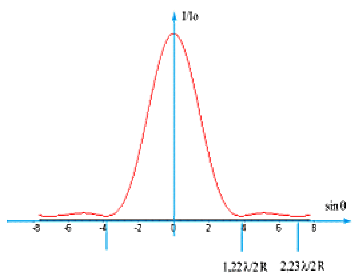
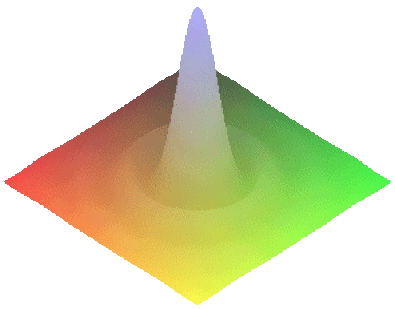
La tache centrale a un rayon angulaire sensiblement double de celui des taches secondaires.
Cette tache centrale bien plus brillante que les anneaux qui l'entourent s'appelle la tache d'Airy. C'est là que se trouve concentrée presque toute la lumière.
Si \(\theta_{rd}\) est faible alors le rayon angulaire de la tache d'Airy est :
\(\sin \theta_1 \approx \theta_1 \approx 1,22 ~.~ \frac{\lambda}{R}\).
L'intensité relative du premier anneau est \(1,75 ~.~ 10^{-2}\) et celle du deuxième anneau \(0,41 ~.~ 10^{-2}\) donc bien plus faible que celle de la tache d'Airy.
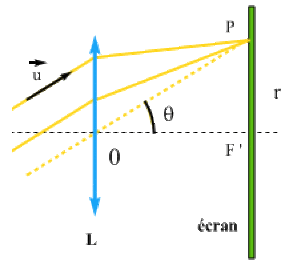
Si l'on observe la figure de diffraction dans le plan focal d'une lentille convergente \(L\), de distance focale \(f'\), les rayons des anneaux observés sont donnés par :
\(r = f' . \theta\) si \(\theta\) est faible.