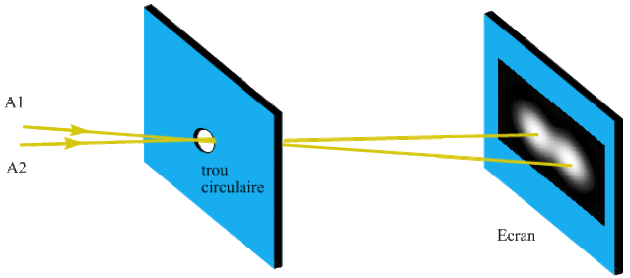
Pouvoir séparateur des instruments d'optique
Deux objets ponctuels \(A_1\) et \(A_2\) peuvent être séparés si les taches de diffraction correspondantes sont séparées.
Observons ce qui se passe lorsque l'écart angulaire entre les objets ponctuels \(A_1\) et \(A_2\) évolue :
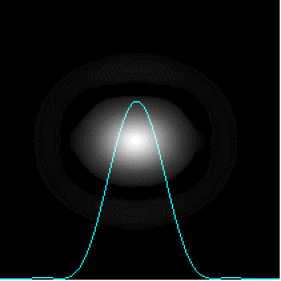
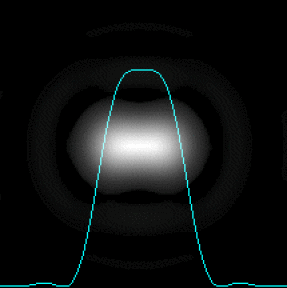
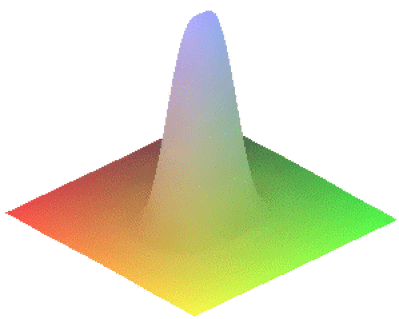
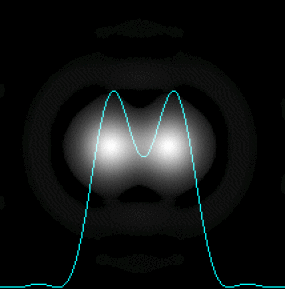
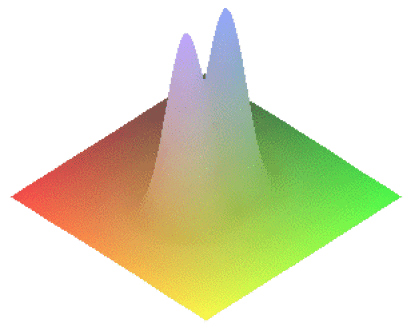
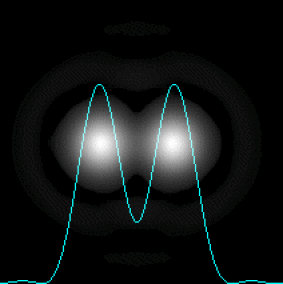
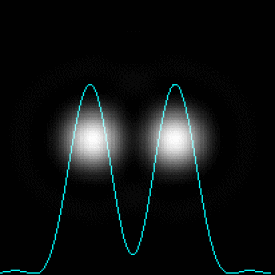
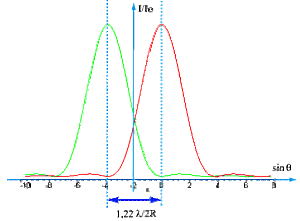
Le critère de Rayleigh donne les conditions limites de séparation des taches de diffraction dont les rayons angulaires sont \(\theta_1\) et \(\theta_2\).
Deux images \(A_1'\) et \(A_2'\) sont séparées si, pour les taches de diffraction correspondantes, le maximum principal de l'une est confondu avec le premier minimum nul de l'autre.
Soit si \(\theta_{rd}\) est faible, ce qui est souvent le cas :
\(\Delta \theta = |\theta_{1 ~ max} - \theta_{2 ~ max}| \ge 0,61 ~.~ \frac{\lambda}{R}\)
Cette valeur est à comparer avec celles données par d'autres contraintes telles la taille des cellules rétiniennes, la taille des grains d'une émulsion photo ,etc.. de manière à évaluer ce qui pratiquement limitera la résolution des instruments d'optique, qu'ils soient subjectif ou objectif.