Présentation classique

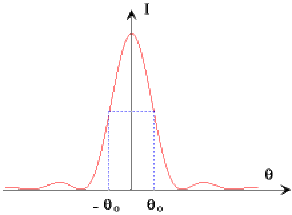
Si \(\theta_0\) représente la position angulaire, comme \(\theta_0\) est petit alors \(\sin \theta_0 = \theta_0\) et donc

\(\displaystyle{I = I_0 \Big( \sin \frac{\pi a \theta_0}{\lambda} \Big) . \left( \frac{1}{\frac{\pi a \theta_0}{\lambda}} \right)^2}\)

Pour \(\theta_0\) \(~~ I = \frac{I_0}{2}\) \(~~ \Rightarrow \frac{\pi a \theta_0}{\lambda} = \pm 1,4 ~\mathrm{rd}\)

\(a = 1,4 . \frac{\lambda}{\pi \theta_0} = \frac{1,5 ~.~ 0,5 . 10^{-6}}{3,14 . \frac{5 . 10^{-3}}{2}} = 95 . 10^{-6} ~ \mathrm m = 1 ~ \mathrm{mm}\)