Equilibre de charges
Partie
Question
Deux charges positives ponctuelles \(q_1=3.10^{-8} ~ \mathrm C\) et \(q_2 =6.10^{-8} \mathrm C\) sont fixes et maintenues à une distance \(d=0,5 ~ \mathrm m\).
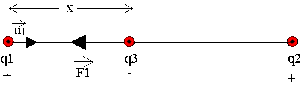
A quelle distance \(x\) de \(q_1\) faut-il placer une charge négative \(q_3\) pour qu'elle soit en équilibre sous l'action des forces exercées par \(q_1\) et \(q_2\) ?
Aide simple
Faites un dessin et représentez les forces électrostatiques exercées par \(q_1\) et \(q_2\) sur \(q_3\).
Aide détaillée
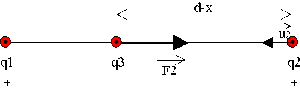
Les forces \(\vec F_1\) et \(\vec F_2\) exercées par \(q_1\) et \(q_2\) sur \(q_3\) sont opposées et leur module est donné par la formule de Coulomb.
Rappel de cours
Voir la page Loi de Coulomb
Solution simple
\(x = 0,207 ~ \mathrm m\)
Solution détaillée
La charge \(q_3\) doit être placée à une distance telle que la force électrostatique exercée par la charge \(q_1\) soit égale et opposée à la force électrostatique exercée par \(q_2\) sur \(q_3\) . Remarquons que \(q_3\) ne peut être placée qu'entre \(q_1\) et \(q_2\). A l'extérieur de ce segment elle serait attirée par \(q_1\) (à gauche) ou \(q_2\) (à droite) donc il n'y aurait pas équilibre.
\(\vec F_1 = \frac{q_1 ~ q_3}{4 \pi \epsilon_0 ~ x^2} \vec u_1\)
\(\vec F_2 = \frac{q_2 ~ q_3}{4 \pi \epsilon_0 ~(d - x)^2} \vec u_2\)
A l´équilibre :
\(\vec F_1 + \vec F_2 = 0\) donc \(\frac{q_1 ~ q_3}{4 \pi \epsilon_0 ~ x^2} \vec u_1 ~ + ~ \frac{q_2 ~ q_3}{4 \pi \epsilon_0 ~(d - x)^2} \vec u_2 = 0\) avec \(\vec u_1 = - \vec u_2\)
On obtient une équation du 2ème degré :
\(x^2 (q_1 - q_2) - 2dxq_1 + d^2 q_1 = 0\)
dont la racine positive est : \(x = 0,207 ~ \mathrm m\)