Définition
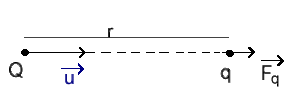
Que l'on approche une charge \(q\) ou une charge \(q'\) à une distance \(r\) d'une charge source \(Q\), la loi de Coulomb indique que :
\(\frac{\overrightarrow F_{q}}{q} = \frac{\overrightarrow F_{q'}}{q'} = \frac{Q}{4 \pi \epsilon_0 ~ r^2} \vec u\)
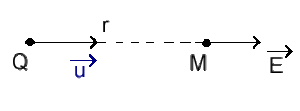
Le rapport \(F/q\) est indépendant de \(q\) ou \(q'\) ; il ne dépend que de la charge source \(Q\) et de la distance par rapport à cette source. On l'appelle champ électrostatique \(\vec E\).
\(\vec E\) est le champ électrostatique créé par la charge source \(Q\) en un point \(M\) de l'espace situé à une distance \(r\). \(\vec E\) traduit localement en tout point \(M\) la modification des propriétés de l'espace due à la présence de la charge source \(Q\).
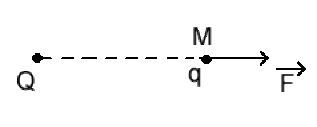
La force électrostatique s'exerçant sur une charge cible \(q\) placée en \(M\) s'exprime alors par :
\(\vec F = q ~ \vec E\)