Travail élémentaire
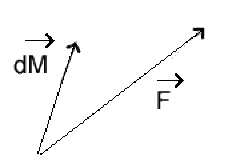
Soit une force \(\vec F\) dont le point d'application effectue un déplacement rectiligne, infiniment petit \(\mathrm d \vec M\).
Le déplacement étant infiniment petit, on peut considérer que la force est constante en cours du déplacement. Par définition, le travail de cette force est le produit scalaire
\(\mathrm d W = \vec F~.~\mathrm d \vec M\)
Le travail \(dW\) est positif si l'angle formé par les vecteurs \(\vec F\) et \(\mathrm d \vec M\) est aigu : on dit alors que ce travail est moteur parce que la force tend à faire se mouvoir le point sur lequel elle s'exerce dans le sens du déplacement \(\mathrm d \vec M\). Si l'angle formé par les vecteurs \(\vec F\) et \(\mathrm d \vec M\) est obtus, le travail est négatif ; il est dit résistant parce que la force tend à s'opposer au déplacement \(\mathrm d \vec M\) du point sur lequel elle s'exerce.