Travail le long d'un contour
Soit maintenant une force dont le point d'application décrit une courbe (\(C\)) quelconque, cette force pouvant varier au cours du temps.
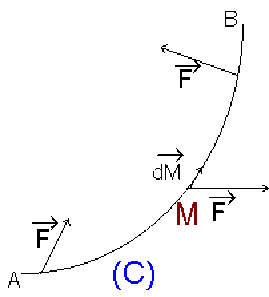
On considère que le déplacement du point d'application \(M\) de la force sur la courbe (\(C\)) consiste en une succession de déplacements élémentaires.
Pour chaque déplacement élémentaire \(\mathrm d \vec M\), on calcule le produit scalaire \(\vec F~.~\mathrm d \vec M\) et on fait la somme des produits scalaires obtenus pour tous les déplacements élémentaires conduisant sur la courbe (\(C\)) du point \(A\) au point \(B\).
Cette somme est par définition le travail \(W\) de la force \(\vec F\) , son point d'application décrivant la courbe (\(C\)) du point \(A\) jusqu'au point \(B\).
Comme chaque déplacement \(\mathrm d \vec M\) est infiniment petit, le travail s'obtient en faisant la somme d'un nombre infini de termes, chacun d'eux étant infiniment petit.
Cette somme est donc une intégrale, que l'on appelle intégrale curviligne, parce qu'elle est calculée sur une courbe. On écrit :
\(W = \int_{(C)} \vec F . \mathrm d \vec M\)