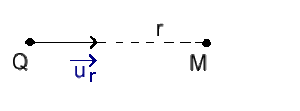
V créé par une charge ponctuelle
A une distance \(r\) d'une charge \(Q\), le potentiel électrostatique en \(M\) est donné par :
\(\displaystyle{V(M) - V_{ref} = - \int \vec E. \mathrm d \vec M}\)
L'influence de \(Q\) devenant négligeable lorsque la distance tend vers \(\infty\), il est légitime d'écrire : \(V(\infty) = 0\).
\(\displaystyle{V(M) = - \int_{\infty}^M \vec E. \mathrm d \vec M}\)
Cette circulation ne dépend pas du chemin suivi pour venir de l'infini jusqu'au point \(M\). Le trajet le plus simple est de se déplacer dans la direction radiale : \(\mathrm d \vec M = \mathrm d r~\vec u_r\)
\(\displaystyle{V(M) = - \int_{\infty}^M \frac {Q} {4 \pi \varepsilon_0 r^2} \vec u_r . \mathrm d r~\vec u_r = - \frac {Q} {4 \pi \varepsilon_0} \int_{\infty}^{r_M} \frac {\mathrm d r} {r^2}}\)
\(V(M) = \frac {Q} {4 \pi \varepsilon_0 r}\)