V créé par une source quelconque
Cas d'une distribution discrète
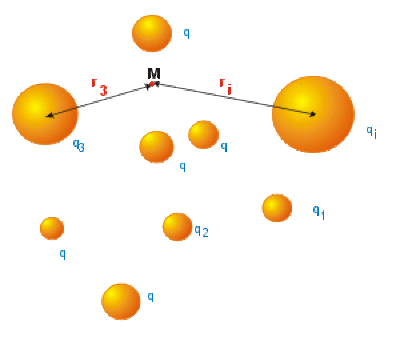
Le champ créé en \(M\) par cette distribution est la somme vectorielle de tous les champs créés en \(M\) par chacune des charges \(q_i\)
D'où le potentiel créé en \(M\) par la distribution est :
\(\displaystyle{V(M) = - \int_{\infty}^M \sum \vec E_i . \mathrm d \vec M = - \int_{\infty}^{r_i} \sum \frac {Q_i} {4 \pi \varepsilon_0 r_i} \vec u_{r_i} . \mathrm d r~\vec u_{r_i}}\)
\(V(M) = \sum_i \frac {Q_i} {4 \pi \varepsilon_0 r_i}\)
Cas d'une distribution continue
nuage de charges

surface électrisée

fil chargé
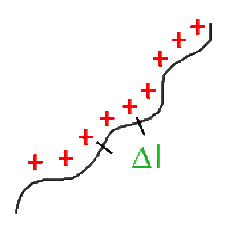
Dans ce cas, la source est découpée en charges élémentaires \(\mathrm d Q\) infiniment petites. Chaque charge élémentaire crée en \(M\) un potentiel :
\(\mathrm d V(M) = \frac{\mathrm d Q}{4 \pi \varepsilon_0 r}\)
et
\(\displaystyle {V(M) = \int_{\mathrm{source}} \frac {\mathrm d Q} {4 \pi \varepsilon_0 r}}\)