Condensateur Plan 1/3
Partie
Question
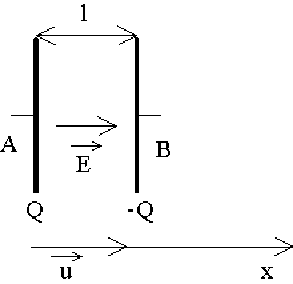
Un condensateur plan est formé de deux plaques métalliques dont l'écartement \(l\) est faible vis-à-vis de leurs dimensions. Ces plaques portent des charges \(-Q\) et \(+Q\) égales et de signe opposé, réparties uniformément sur leur surface \(S\), avec des densités superficielles de charges respectivement de :
\(- \sigma = - Q/S\) et \(+ \sigma = + Q/S\) .
Le champ électrostatique créé par une telle structure est la résultante des champs créés par chacune des plaques et a pour expression dans la région comprise entre les plaques (loin de leurs bords)
\(\vec E = \frac{\sigma}{\epsilon_0} \vec u\) ,
le vecteur unitaire \(\vec u\) étant dirigé de la plaque positive (conducteur \(A\)) vers la plaque négative (conducteur \(B\)).
Aide simple
Définition du potentiel
\(\displaystyle{V(A) - V(B) = - \int_B^A \vec E . \mathrm d \vec M}\)
\(\mathrm d \vec M\) est un déplacement élémentaire entre les deux conducteurs.
Aide détaillée
\(\mathrm d \vec M\) est un déplacement élémentaire le long d'un contour réunissant les deux plaques. Le calcul de la différence de potentiel ne dépendant pas du trajet suivi, il est plus simple de choisir un trajet parallèle à l'axe \(Ox\).
Dans ce cas :
\(\mathrm d \vec M = \mathrm d x ~ \vec u\)
Rappel de cours
Voir la page Définition
Solution simple
\(V(A) - V(B) = \frac{Q}{\epsilon_0 S} l\)
Solution détaillée
La différence de potentiel \(V(A) - V(B)\) peut aisément se calculer ; \(\mathrm d \vec M\) est un déplacement le long d'un contour réunissant les deux plaques. Le calcul de la différence de potentiel ne dépendant pas du trajet suivi, il est plus simple de choisir un trajet parallèle à l'axe \(Ox\).
Dans ce cas :
\(\mathrm d \vec M = \mathrm d x ~ \vec u\)
\(\displaystyle{V(A) - V(B) = - \int_{B}^{A} \vec E . \mathrm d \vec M = - \int_{B}^{A} \frac{\sigma}{\epsilon_0} \vec u ~ \mathrm d x ~ \vec u = - \int_{x_B}^{x_A} \frac{\sigma}{\epsilon_0} \mathrm d x = \frac{\sigma}{\epsilon_0}(x_B - x_A) = E ~ l}\) ,
\(l\) étant la distance entre les plaques.
\(V(A) - V(B) = \frac{Q}{\epsilon_0 S} l\)