Exercice 3
Durée : 3 mn
Note maximale : 10
Question
L'affirmation suivante est-elle vraie ?
" En tout point d'une surface équipotentielle le champ a même valeur en module "
Solution
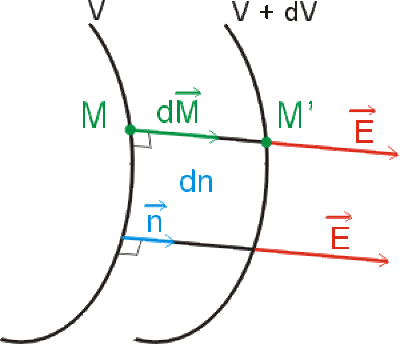
Entre deux points \(M\) et \(M'\) respectivement portés par les équipotentielles de potentiel \(V\) et \(V+dV\) : \(dV=-\vec E.d\vec M\).
Le champ \(\vec E\) est porté par la normale aux équipotentielles \(\vec E=E.\vec n\). Sur la normale aux équipotentielles : \(d\vec M=dn.\vec n\)
\(dV=-Edn\Rightarrow E=-\frac{dV}{dn}\) Le module du champ n'est pas constant. Il est inversement proportionnel à l'écartement des équipotentielles : le champ est d'autant plus intense que les équipotentielles sont resserrées.
\(E > 0\) si \(dV < 0\)
\(\vec E\) est dirigé vers les potentiels décroissants. 10 pts