Champ créé par un disque chargé 1/1
Partie
Question
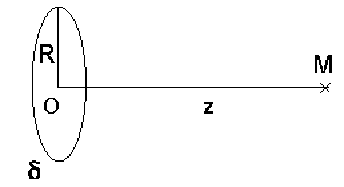
Soit un disque de rayon \(R\) chargé par une densité superficielle de charges \(\sigma\) uniforme.
Le potentiel en un point \(M\) de l'axe à la distance \(z\) est donné par : \(V=\frac{\sigma}{2\epsilon_0}(\sqrt{R^2+z^2}-z)\).
a) Quelle est la direction du champ \(\vec E\) au point \(M\) ?
b) Quelle est l'expression de \(\vec E\) au point \(M\) ?
Solution détaillée
\(V\) ne dépend que de \(z\), le champ qui est égal à \(\overrightarrow{\mathrm {grad}} ~ V\) ne peut avoir qu'une composante suivant l'axe \(Oz\) :
\(E_z=-\frac{\partial V}{\partial z}=\frac{\sigma}{2\epsilon_0}\left(1-\frac{z}{\sqrt{R^2 + z^2}}\right)\)
\(\vec E=\frac{\sigma}{2\epsilon_0}\left(1-\frac{z}{\sqrt{R^2+z^2}}\right)\vec u_z\)